DATA MINING TUTORIAL
64 Posts
NUMBER SYSTEM
274 Posts
POLITICS
120 Posts
JAVASCRIPT INTERVIEW QUESTIONS
59 Posts

Can’t find an answer?
Ask us to get the answer
- This forum is empty.
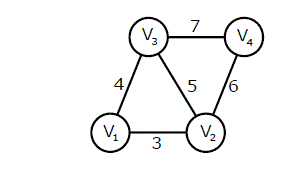
An undirected graph G(V, E) contains n ( n > 2 ) nodes named v1 , v2 ,….vn. Two nodes vi , vj are connected if and only if 0 < |i – j| <= 2. Each edge (vi, vj ) is assigned a weight i + j. A sample graph with n = 4 is shown below. What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes? (GATE CS 2011)
(A) 1/12(11n^2 – 5n)
(B) n^2 – n + 1
(C) 6n – 11
(D) 2n + 1
Consider the following graph:
Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm?
(A) (a—b),(d—f),(b—f),(d—c),(d—e)
(B) (a—b),(d—f),(d—c),(b—f),(d—e)
(C) (d—f),(a—b),(d—c),(b—f),(d—e)
(D) (d—f),(a—b),(b—f),(d—e),(d—c)
- You must be logged in to create new topics.