InterviewSolution
Saved Bookmarks
| 1. |
A circle passing through the vertex C ofa rectangle ABCD and touching its sides AB and AD at M and N, respectively. If the distance from C to the line segment MN is equal to 5 units, then find the area of the reactangle ABCD. |
|
Answer» <P> Solution :Let us take AB and AD as coordinate axes.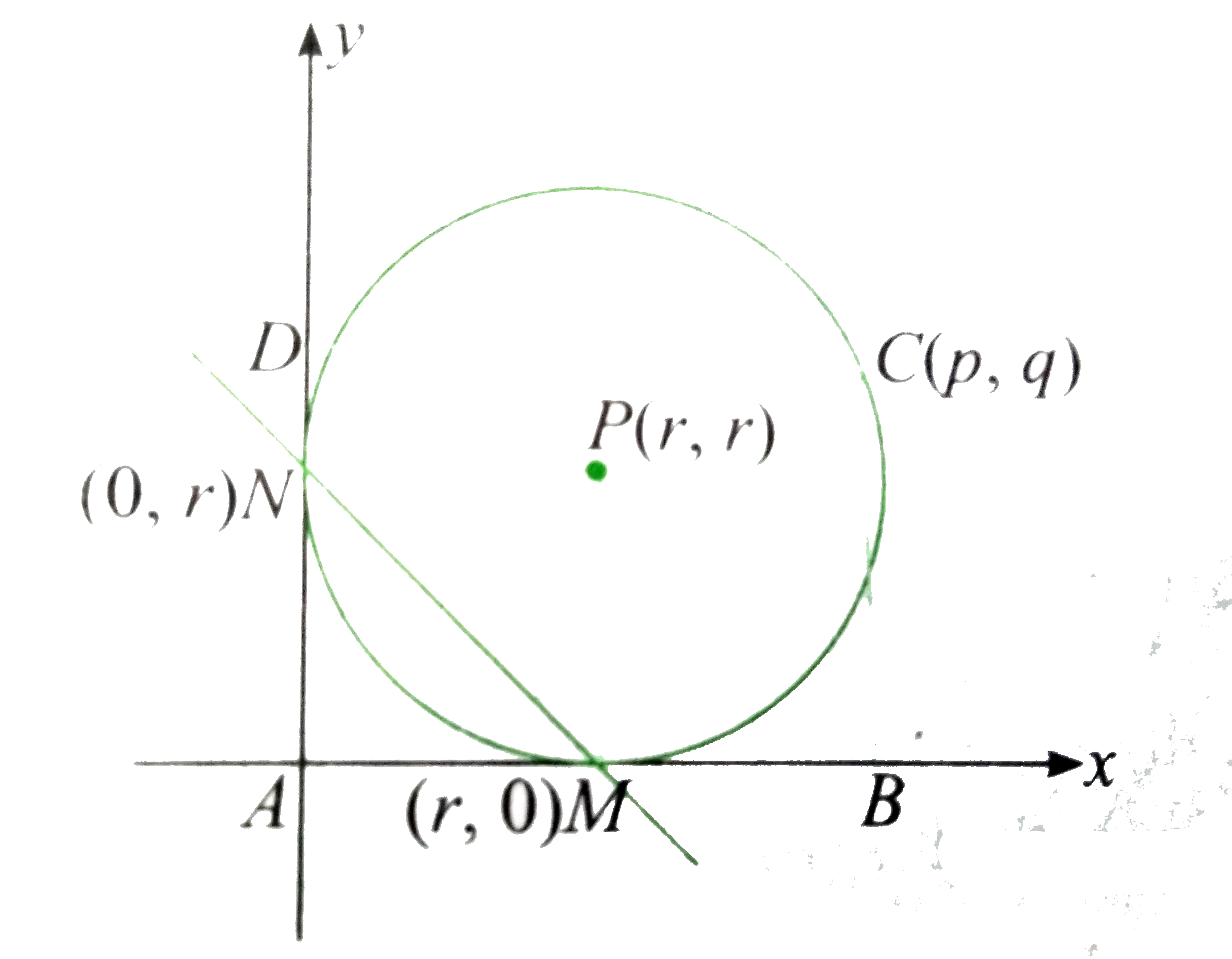 If r is the radius of CIRCLE , then equation of circle touching both the axes is `(x-r)^(2)+(y-r)^(2)=r^(2)` or `x^(2)+y^(2)-2rx-2ry+r^(2)=0` Let point C be (p,q) Equation of line MN is `x+y-r=0` DISTANCE of MN from C is 5 units. `:. (|p+q-r|)/(sqrt(2))=5` `implies (p+q-r)^(2)=50` Since (p,q) lies on the circle , we have `p^(2)+q^(2)-2rp-2rq+r^(2)=0` `implies (p+q-r)^(2)-2pq=0` `implies 50-2pq=0` `implies pq=25` Therefore, area of rectangle `25sq.` units. |
|