A company makes 3 model of calculators, A, B and C at factory I and factory II. The company has orders for atleast 6400 calculators of model A, 4000 calculators of model 8 and 4800 calculators of model C. Atfactory I, 50 calculators of model A, 50 of model 8 and 30 of model C are made everyday, at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs ? 12000 and 1 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.

A company makes 3 model of calculators, A, B and C at factory I and fa

1.	A company makes 3 model of calculators, A, B and C at factory I and factory II. The company has orders for atleast 6400 calculators of model A, 4000 calculators of model 8 and 4800 calculators of model C. Atfactory I, 50 calculators of model A, 50 of model 8 and 30 of model C are made everyday, at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs ? 12000 and 1 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
Answer» Solution :Let the factory I operate for x days and the factory II operate for y days.At factory l, 50 calculators of model A and at factory II, 40 calculators of model A are madeeveryday. Also, company has ordered for atleast 6400 calculators of model A. `50x+40 ge 6400 Rightarrow 5x +4Y ge 640 ,.....(i)` Also, at factory l, 50 calculators of model 8 and at factory II, 20 calculators of modal 8 are made everyday Since, the company has ordered atleast 4000 calculators of model B `therefore 50x+20y ge 4000 Rightarrow 5x+2y ge 4000...(ii)` Similarly for model C, 30x+40y ge 4800 `Rightarrow 3x+4y ge 480 ...(iii)` Also,`x ge 0, y ge 0 ...(iv)["Since x and y are non negative"]` If costs 12000 and 15000 each day to operate factories I and II respectively. Corresponding LPP is Minimise Z=12000x+15000y, "subject to" `5x+6y ge 640` `5x+2y ge 480` `3x+4y ge 480` `x ge 0, y ge 0` on solving 3x+4y=480 and 5x+4y=640, we get x=80, y=60 On solving 5x+4y=640, we get x =32, y=120 Thus from the GRAPH it is clear that feasible region is unbounded and the coordinates of corner points A,B,C and D are (160,0),(80,60),(32,120) and (0,200) respectively 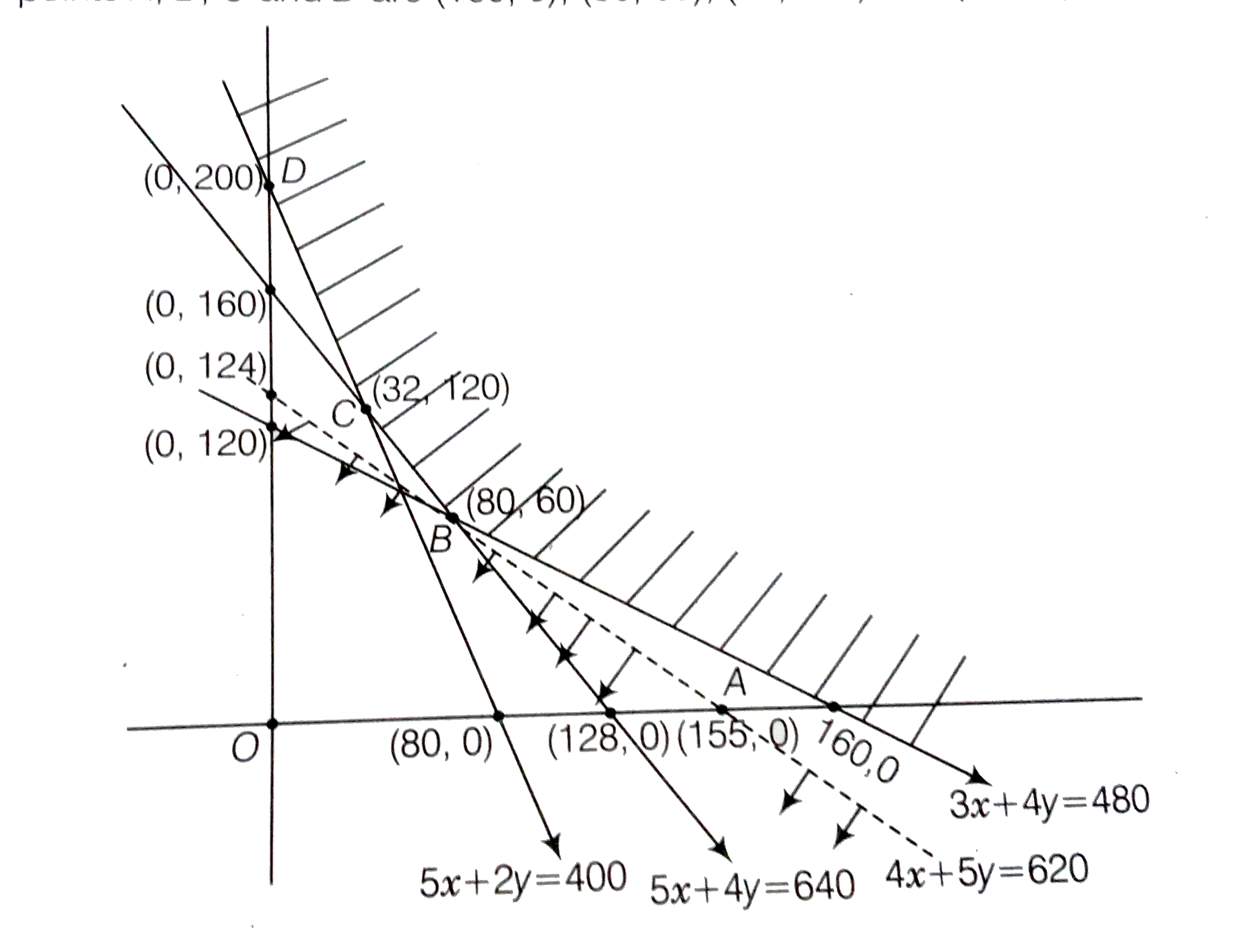From the above table, it is clear that for given unbouded region the minimum valur of Z may or may not be 1860000. Now for deciding this, we graph, the inequality 12000x+15000y lt 1860000 `4x+5y lt 620` and check whether THERESULTING open half plane has points in common with feasible region or not. Thus, as shown in the figure it has no common points so, Z=12000x+15000y has minimum value 1860000. Som number of day factory I should be operated is 80 and number of days factory II should be operated is 60 for the minimum cost and SATISFYING the given constraints.

Discussion

No Comment Found

Related InterviewSolutions

P (-2,-1) and (0,-3) are the limiting points of a coaxial system of whichC -= x^(2) + y^(2)+ 5x + y + 4 = 0is a member. The circleS -= x^(2) + y^(2) - 4x - 2y - 15 = 0is orthogonal to the circle C . The point where the polar of P cuts the circle S is
Which of the following is/are discontinous at x = 1 ?
Write Minors and Cofactors of the elments of following determinants : |{:(1,0,4),(3,5,-1),(0,1,2):}|
The vertex of the parabola (y-1)^2 =8 (x-1) is at the centre of a circle and the parabola cuts that circle atthe ends of its latusrectum. Then the equation of that circle is
{{:(5x-3y=10),(6y=kx-42):} In the system of linear equations above, k represents a constant. If the system of equations has no solution, what is the value of 2k?
f(x) ={{:(1-sqrt(1-x^(2)),if -1lexle1),(1+ log ""(1)/(x), if xgt1):}
Given that alpha, beta, gamma, delta are in a geometric progression. If alpha, beta are the roots of x^(2)-x+p=0 " and "gamma, delta are the roots of x^(2)-4x+q=0, where p and q are integers, then the ordered pair (p, q) =
A poor , frustrated artist named Fresco created a plan to make money. He collected trash, repurposed it into sculptures, then asked various celebrities to write and paint on these trash objects, which he then sold on his own as modern high art. The chart below separately showsthe cost and revenue of his plan. The linear cost function, C(x) , represents the total money spent to make and market the art , while the linear revenue function, R(x) , shows the amount of money he has made in sculpture sales. Fresco initially spent money promoting the project in the media . He also had to pay the celebrities to participate . After 6 months , Fresco had created and sold x number of trash sculptures and finally broke even : he hadn't made or lost any money . How many sculptures did Fresco sell in his first 6 months of the project ?
A poor , frustrated artist named Fresco created a plan to make money. He collected trash, repurposed it into sculptures, then asked various celebrities to write and paint on these trash objects, which he then sold on his own as modern high art. The chart below separately showsthe cost and revenue of his plan. The linear cost function, C(x) , represents the total money spent to make and market the art , while the linear revenue function, R(x) , shows the amount of money he has made in sculpture sales. The cost function in the chart is determined by a constant production cost per sculpture - in this case, the amount Fresco pays each celebrity to participate - as well as a fixed cost , or the initial cost of promoting the project . What is the fixed cost of Fresco's trash sculpture project ?
An ellipse is incribed in a rectangle and if the angle between the diagonals is tan ^(-1)2sqrt2then e=

Discussion

No Comment Found

Related InterviewSolutions

Reply to Comment