InterviewSolution
Saved Bookmarks
| 1. |
A company manufacturers two types of novelty suouvenirs made of plywood. Souvenirsof type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs. 5 each for type A and Rs. 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximise the profit? |
Answer» Solution :Let `x` be the souvenirs of A type and `y` of B type be manufacture by the company. Then, 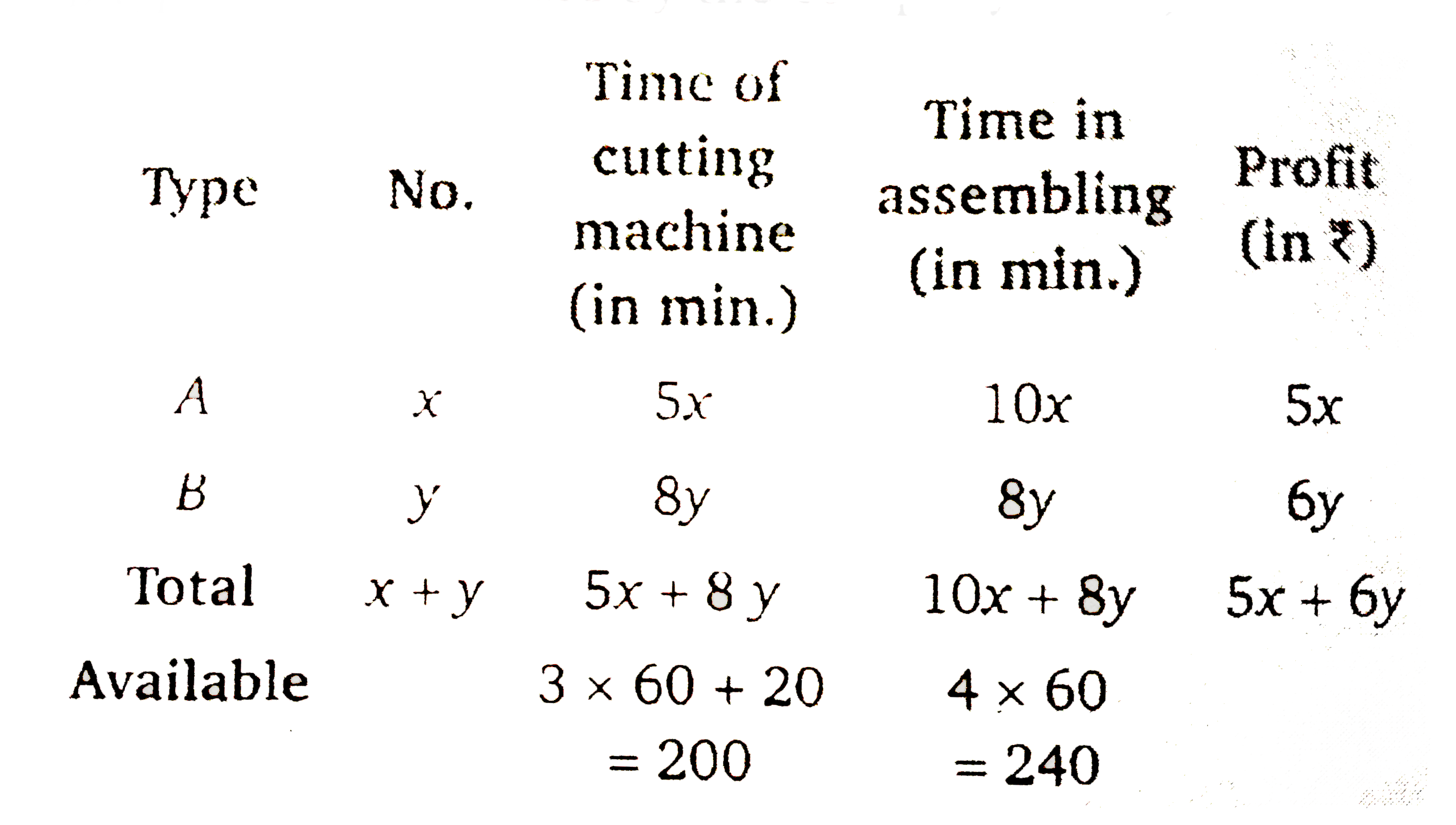 Maximise `Z=5x+6y`……………1 Constraints `5x+8yle200`………………2 `10x+8yle240implies4x+4yle120`………….3 `xge0,yge0`.................4 First, DRAW the graph of first line `5x+8y=200`.  PUT `(0,0)` in the inequation `5x+8yle200`, `5xx0+8xx0le200implies0le200`. (True) Therefore the half plane contains the ORIGIN. Since `x,yge0`.So the feasible region will be in first quadrant. Now, draw the graph of the line `5x+4y=120`. 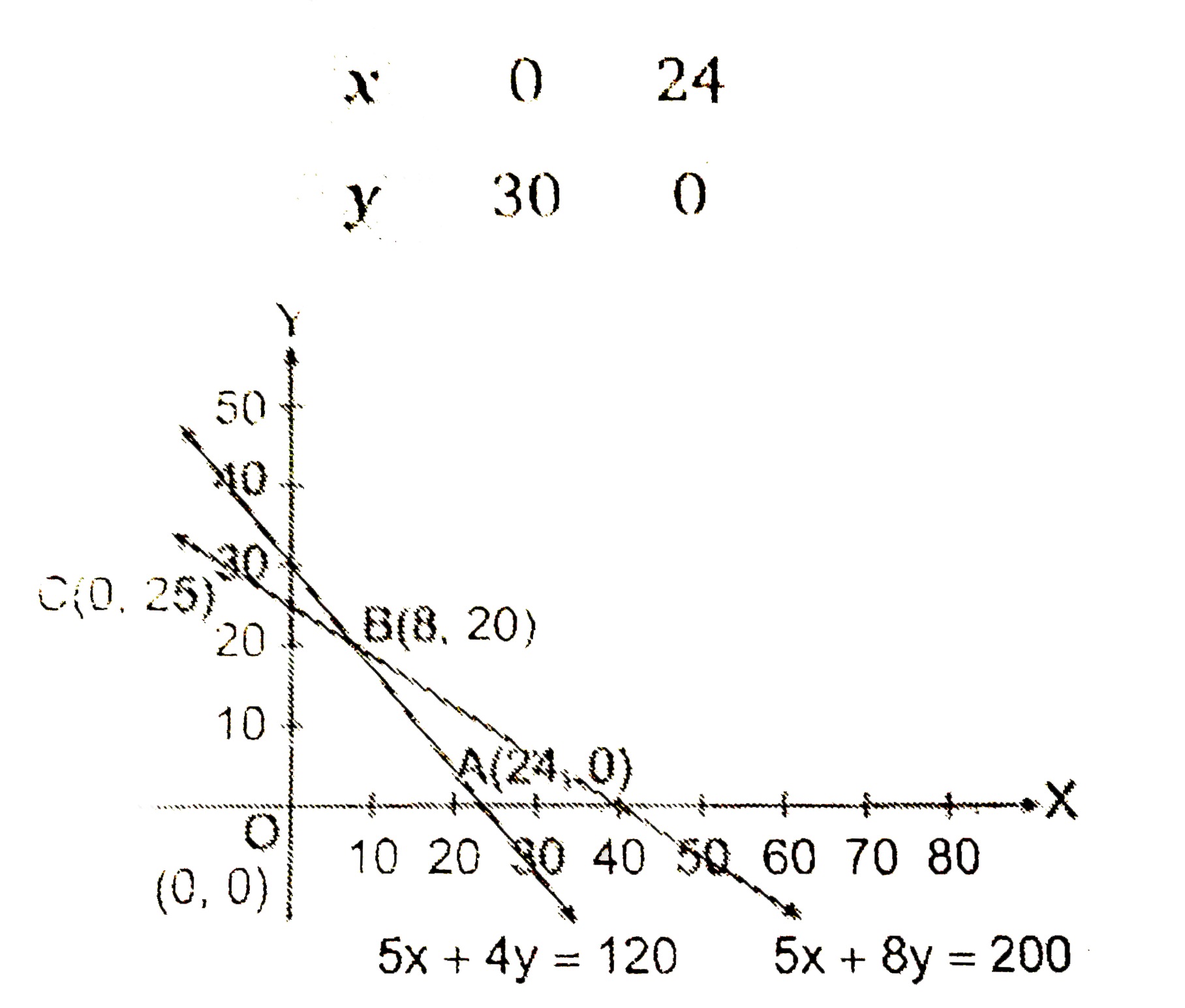 Put `(0,0)` in the inequation `5x+4yle120`, `5xx0+4xx0le120` `implies0le120` (True) Therefore, the half plane contains the origin. From equations `5x+8y=200` and `5x+4y=120`. The point of intersection is `B(8,20)`. `:.` Feasible region is OABCEO. Thus, the vertices of the feasible region are `O(0,0),A(24,0),B(8,20)` and `C(0,25)`. We FIND the value of `Z` at these vertices . 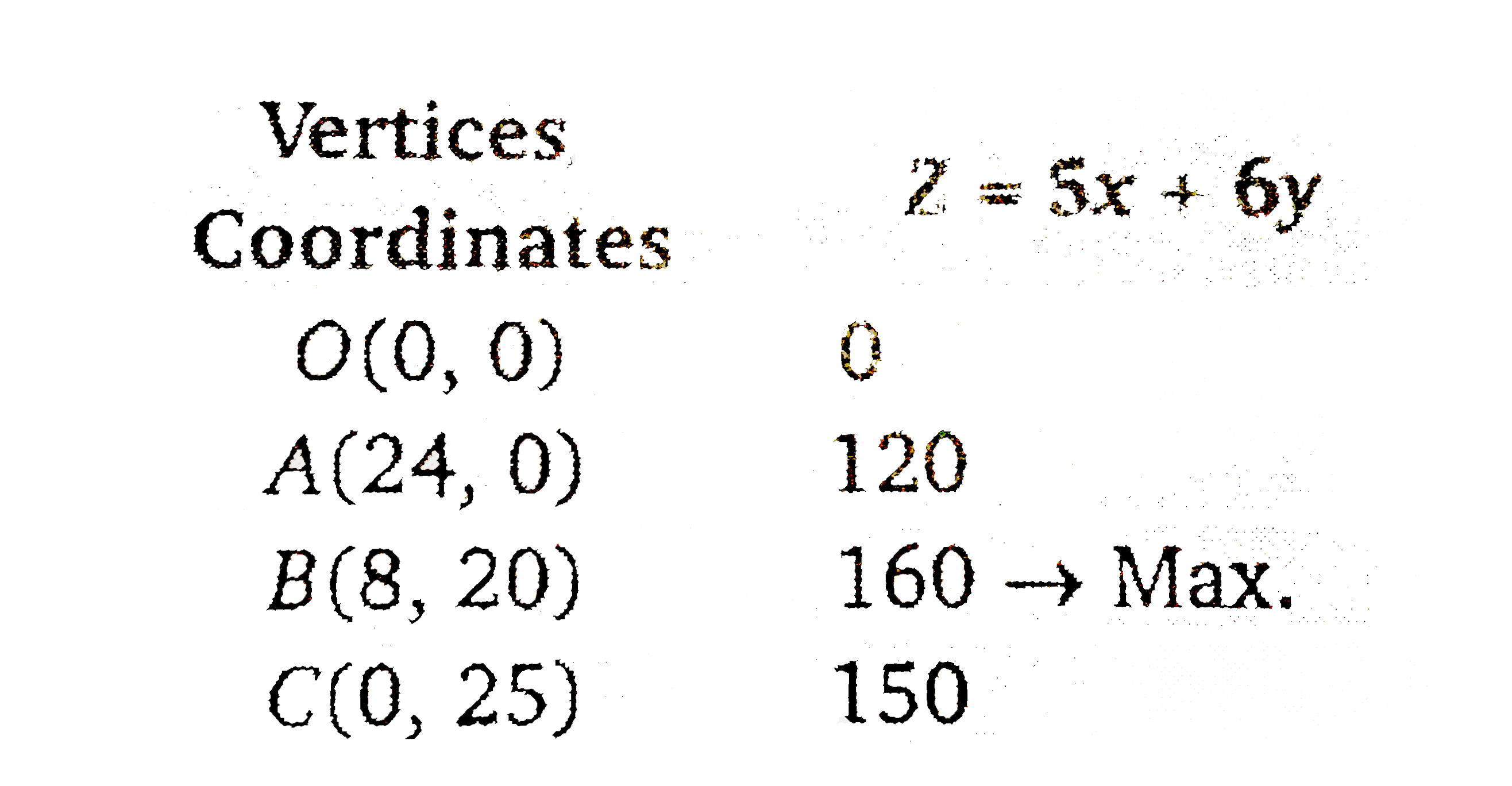 The maximum value of `Z` is Rs. 160 at point `B(8,20)`.Therefore, to obtain the maximum PROFIT Rs. 160 the souvenirs 8 of types of A and 20 of tyes B should be produced. |
|