InterviewSolution
Saved Bookmarks
| 1. |
A companymanufactureis bicyles and tricycleseach of whichmust beprocessed through machines A and B. Machine A hasmaximum of 120 hoursavaiableand machine B hasmaximumof 180 hours available hourson machine A and 3 hourson machine B. Machine A and 10 hourson machine B.Ifprofitare ₹ 180 for a bicyleand ₹ 220 for a tricyle , formulateand solvethe L.P.P to determinethenumberof bicyclesand tricycle that should bemanufactured in orderto maximize the profit . |
Answer» Solution :Let x no. of bicyclesand y no.oftricycleare to be manufactured . Then, total profit Z = (180 x+ 220 y) WHICHIS to bemaximized. From table, we have `6X + 4y le 120 , 3x + 10y le 180` ` x ge 0 ,y ge 0` (`because` no . ofbicycles and tricyles cannot be negative) Themathematicalformulation of given LPP is Maximie Z = 180 x + 220y such that`6x + 4yle 120,` `3x + 10y le 180` `x ge 0 , y ge 0` Now , darw the LINE AB and CD of equations `6x4y = 120` and `3x + 10y = 180` respectively 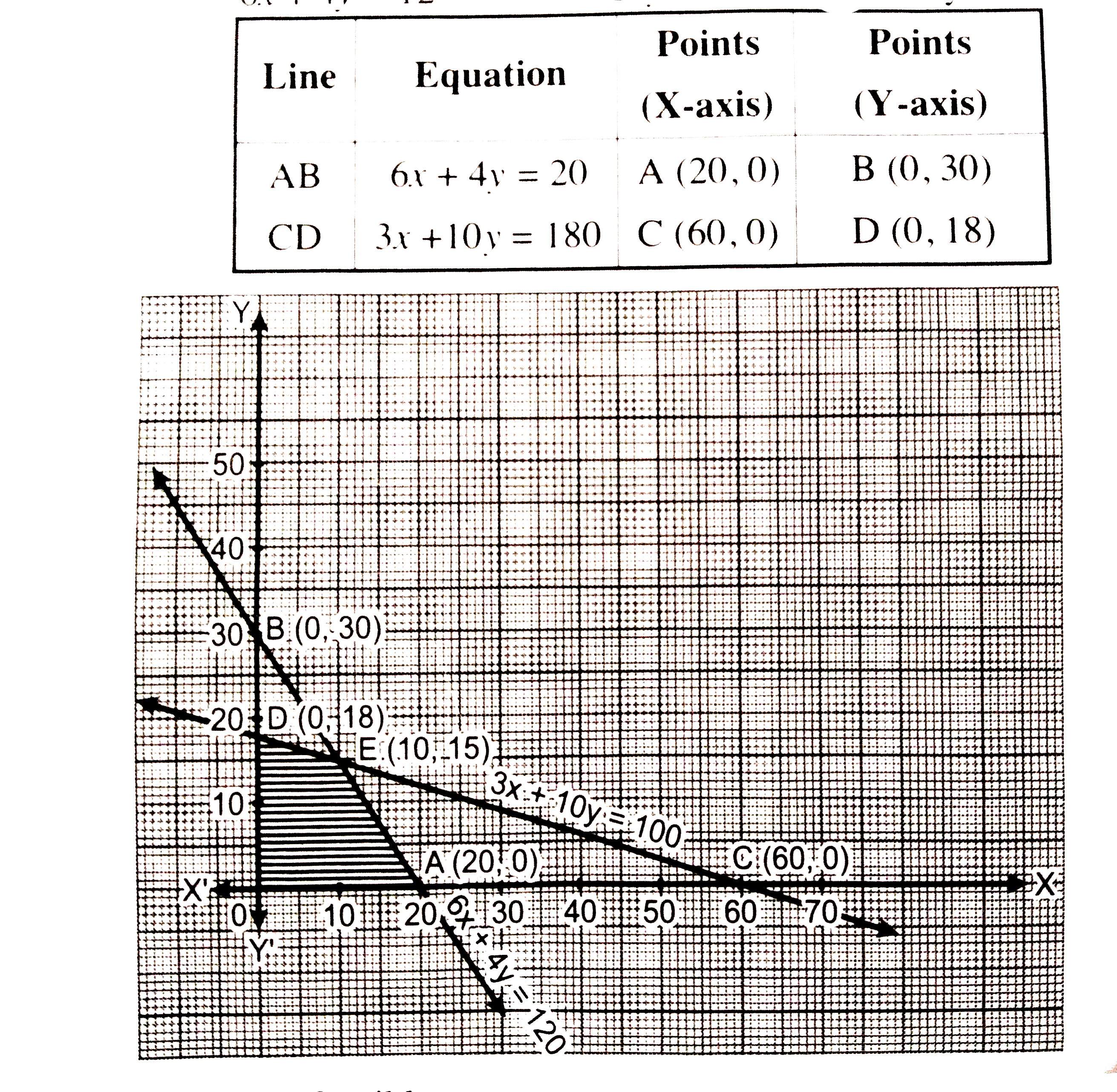 Thefeasibleregion is OAEDO with`O(0,0), A(20,0) E and D (0,18)` E is thepointof intersectionof thelines. `""3x + 10y = 180,"".......(1)` `and""6x + 4y = 120 "".....(2)` Multiplying EQUATION (1) by 2 andsubtracting equation (2) form it , we get `{:(6x + 20y = 360),(6x + 4y = 120),(-" "-" "-),(overline(""16y = 240)):}` `rArr "y = 15` Puttingy= 15 in equation (1), we get x = 10 `therefore E(10, 15)` 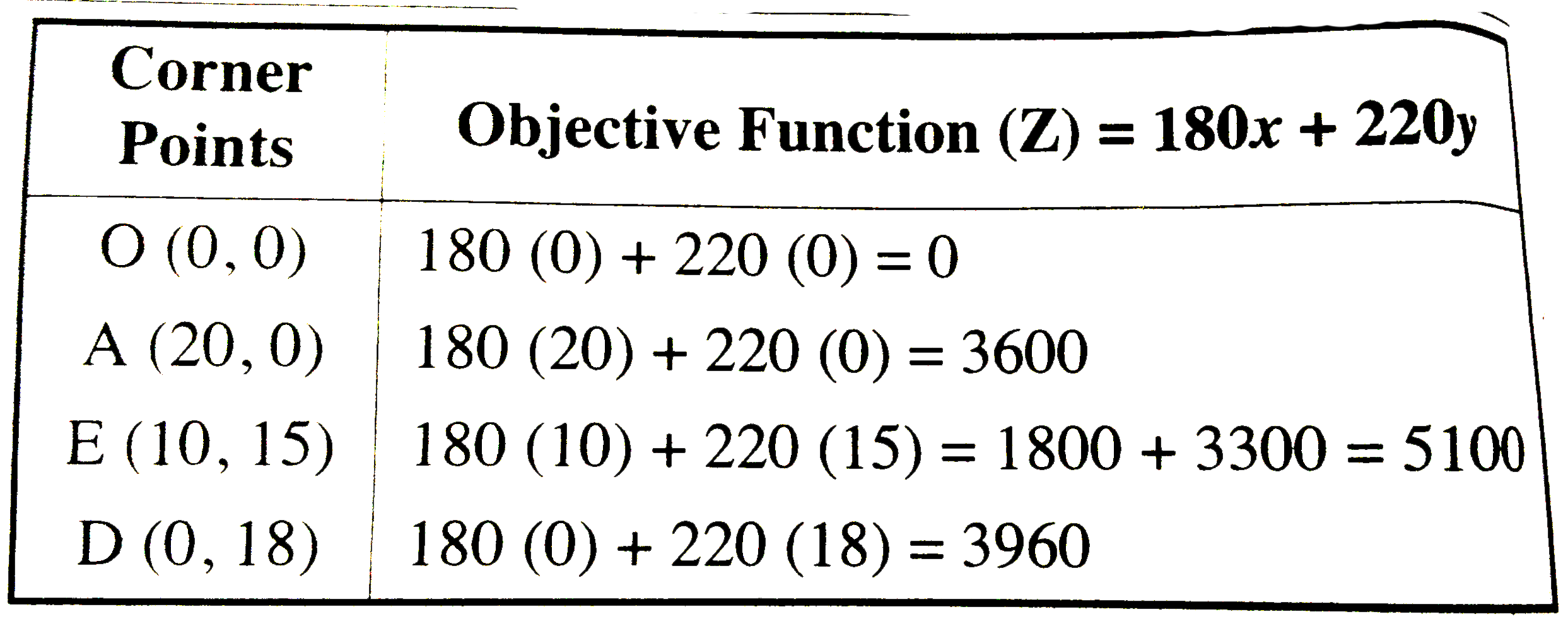 HENCE, the maximum valueof Z is5100 at E (10, 15) i.e.,10 bicyles and15 tricylesshouldbe manufactured to maximize the profit. |
|