InterviewSolution
Saved Bookmarks
| 1. |
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/ cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lam. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hour and the grinding/ cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade isRs. 3. Assuming that the manufacturer can sell all the lamps and shadesthat the produces how should be scehdule his daily production in order to maximise his profit? |
Answer» Solution :Let the MANUFACTURE makes `x` pedestal lamps and `y` wooden shades per day then 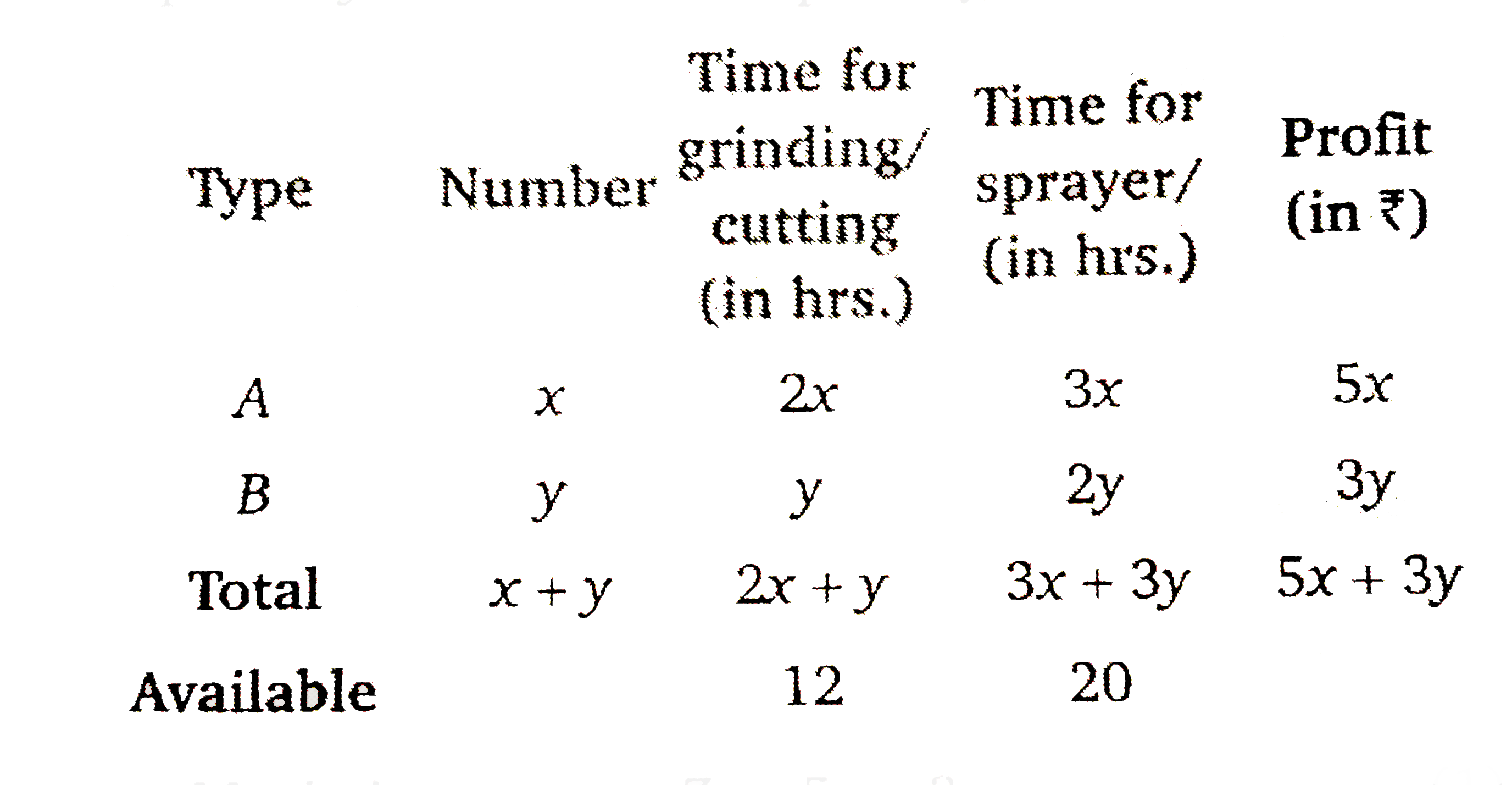 Maximise `Z=5x+3y`…………. 1 Constraints `2x+yle12`…………………2 `3x+2yle20`………………..3 `xge0,yge0`………………….4 First, draw the graph of the equation `2x+y=12`  Put `(0,0)` in the inequation `2x+yle12`, `2xx0+0le12` `0le12` (True) THEREFORE, half plane contain the origin. Since `x,yge0` Therefore FEASIBLE region will be in first quadrant. Now, draw the graph of the line `3x+2y=20`  Put `(0,0)` in the inequation `3x+2yle20` `3xx0+2xx0le20implies0le20` (True) Therefore half plane contains the origin.  From equations `2x+y=12` and `3x+2y=20` The point of intersection is `B(4,4)` Therefore the feasible region is OABCO. Its vertices are `O(0,0),A(6,0),B(4,4)` and `C(0,10)` we FIND the value of `Z` at these vertices.  The maximum value of `Z` is Rs. 32 at point `B(4,4),`. Therefore 4 pedestal LAMP and 4 wooden shade should be made the manufacturer to obtain the maximum profit. |
|