1.

A disc of radius R=10 cm oscillates as a physical pendulum about an axis perpendicular to the plane of the disc at a distance r from its centre. If r=(R)/(4), the approximate period of oscillation is (Take g=10ms^(-2))

Answer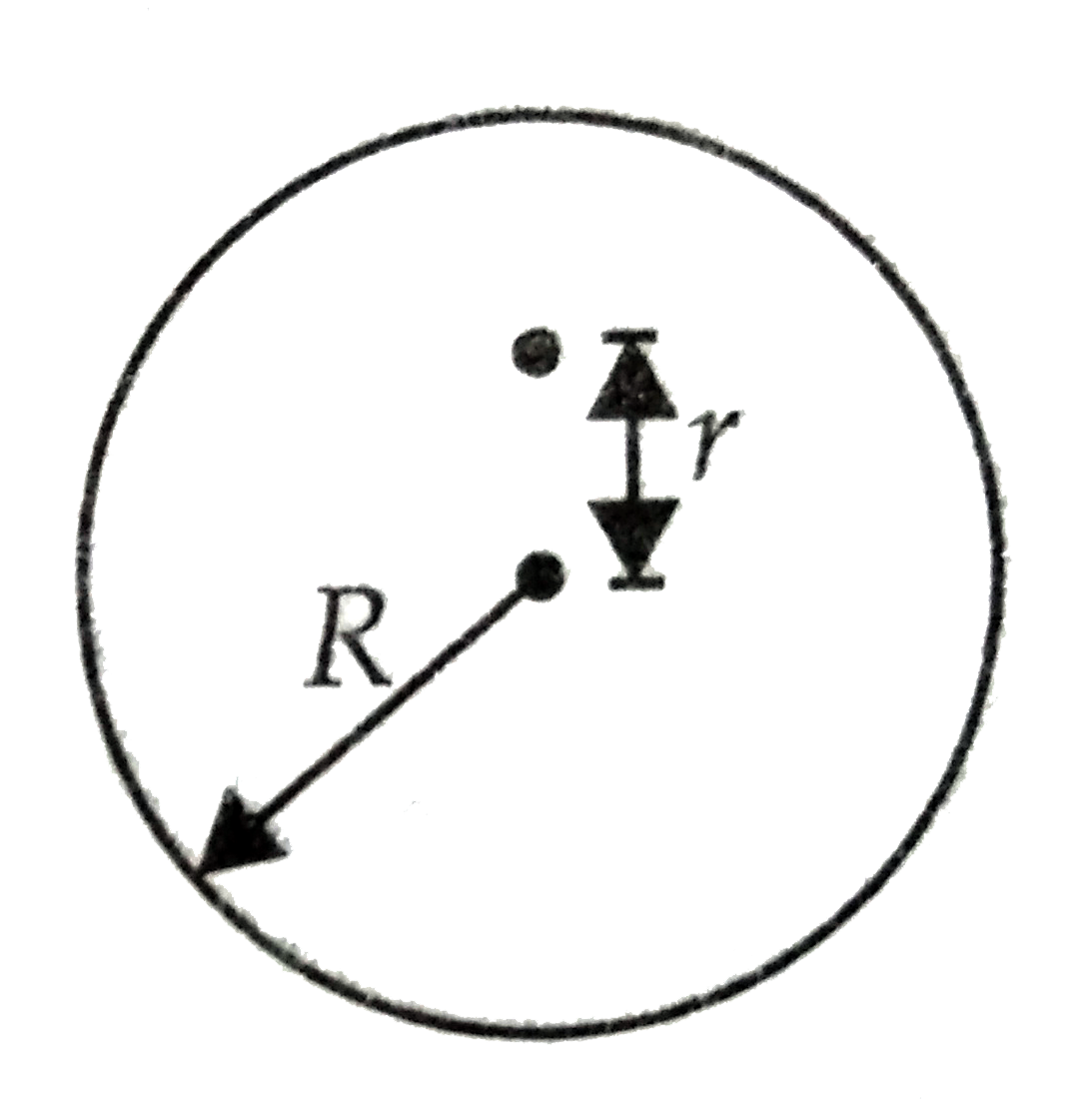» <html><body><p>0.84 s<br/>0.94 s<br/>1.26 s<br/>1.42 s</p>Solution :<img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_OBJ_FING_PHY_XI_C14_E01_082_S01.png" width="80%"/> <br/> `T=2pisqrt((I)/(mgh))` <br/> Where I is the moment of inerrtia of the <a href="https://interviewquestions.tuteehub.com/tag/pendulum-1149901" style="font-weight:bold;" target="_blank" title="Click to know more about PENDULUM">PENDULUM</a> about an axiis through the pivot, <br/> m is the mass of the pendulum and h is the distance from the pivot to the centre of mass. <br/> In this case, a <a href="https://interviewquestions.tuteehub.com/tag/solid-1216587" style="font-weight:bold;" target="_blank" title="Click to know more about SOLID">SOLID</a> disc of R oscillates as a physical pendulum about an axiis perpendicular to the plane of the disc at a distance r from its centre. <br/> `thereforeI=(mR^(2))/(2)+mr^(2)=(mR^(2))/(2)+m((R)/(4))^(2)=(mR^(2))/(2)+(mR^(2))/(16)` <br/> `=(9mR^(2))/(16)""(becauser=(R)/(4))` <br/> Here, `R=10cm=0.1m,h=(R)/(4)` <br/> `thereforeT=2pisqrt(((9mR^(2))/(16))/((mgR)/(4)))=2pisqrt((9R)/(4g)` <br/> `=2pisqrt((9xx0.1)/(4xx10))=2pixx(3)/(2)xx(1)/(<a href="https://interviewquestions.tuteehub.com/tag/10-261113" style="font-weight:bold;" target="_blank" title="Click to know more about 10">10</a>)=0.94s`</body></html>


Discussion

No Comment Found

Related InterviewSolutions