A fruit grower canuse two types of fertilizer in his garden brand P and brand Q. The amounts (in kg) of nitrogen phosphoric acid, potash, and chlorine a bag of each brand are given in the stable. Tests indicate that the garden needs at least 240kg of phosphoric acid, at least 270 kg ofpotash and at most 310 kg of chlorine. If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?

A fruit grower canuse two types of fertilizer in his garden brand P an

1.	A fruit grower canuse two types of fertilizer in his garden brand P and brand Q. The amounts (in kg) of nitrogen phosphoric acid, potash, and chlorine a bag of each brand are given in the stable. Tests indicate that the garden needs at least 240kg of phosphoric acid, at least 270 kg ofpotash and at most 310 kg of chlorine. If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
Answer» Solution :Let `x` bags of brand `P` and `y` of brand `Q` are used by fruit grower. 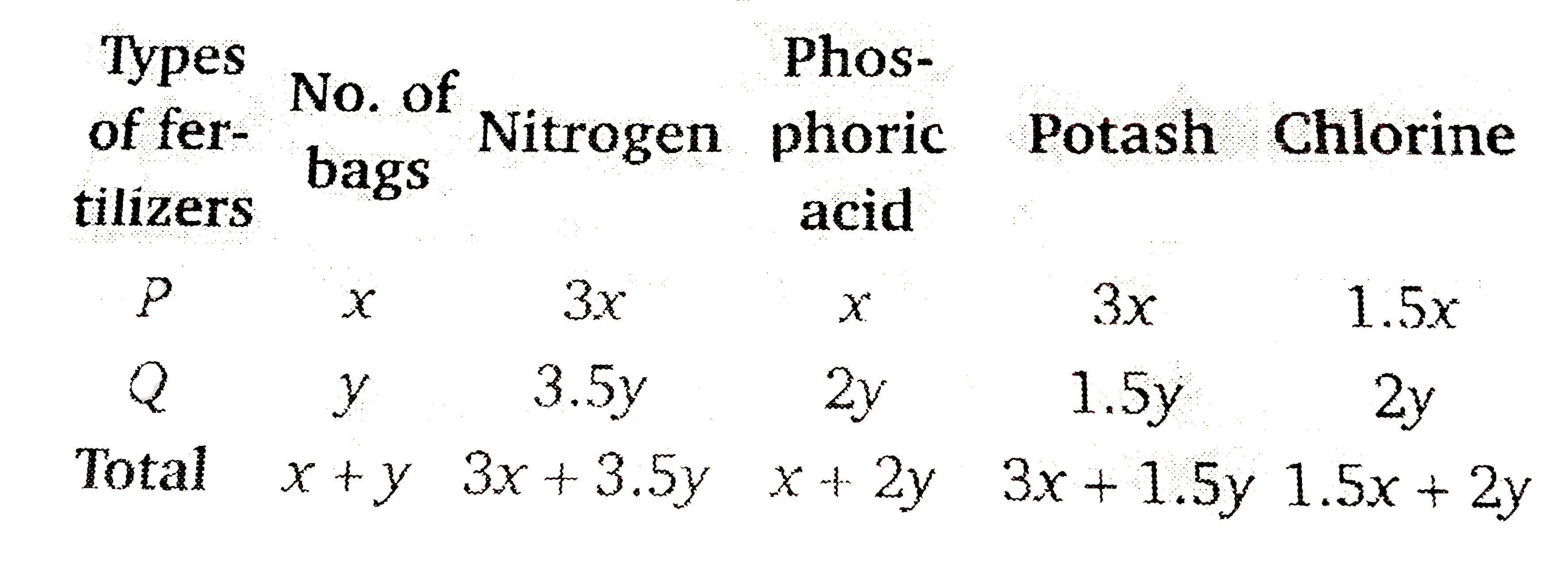Minimise `Z=3x+3.5y`……………1 and constraints `x+2yge240`………………2 `3x+1.5yge270`………………….3 `1.5x+27le310`……………..4 `xge0,yge0`.......................5 FIRST DRAW the graph of the line `x+2y=240` Put `(0,0)` in the inequation `x+2yge240` `0+2xx0ge240implies0ge240` (False) Thus, the half plane does not contain origin. Now, draw the graph of the line `3x+1.5y=270` 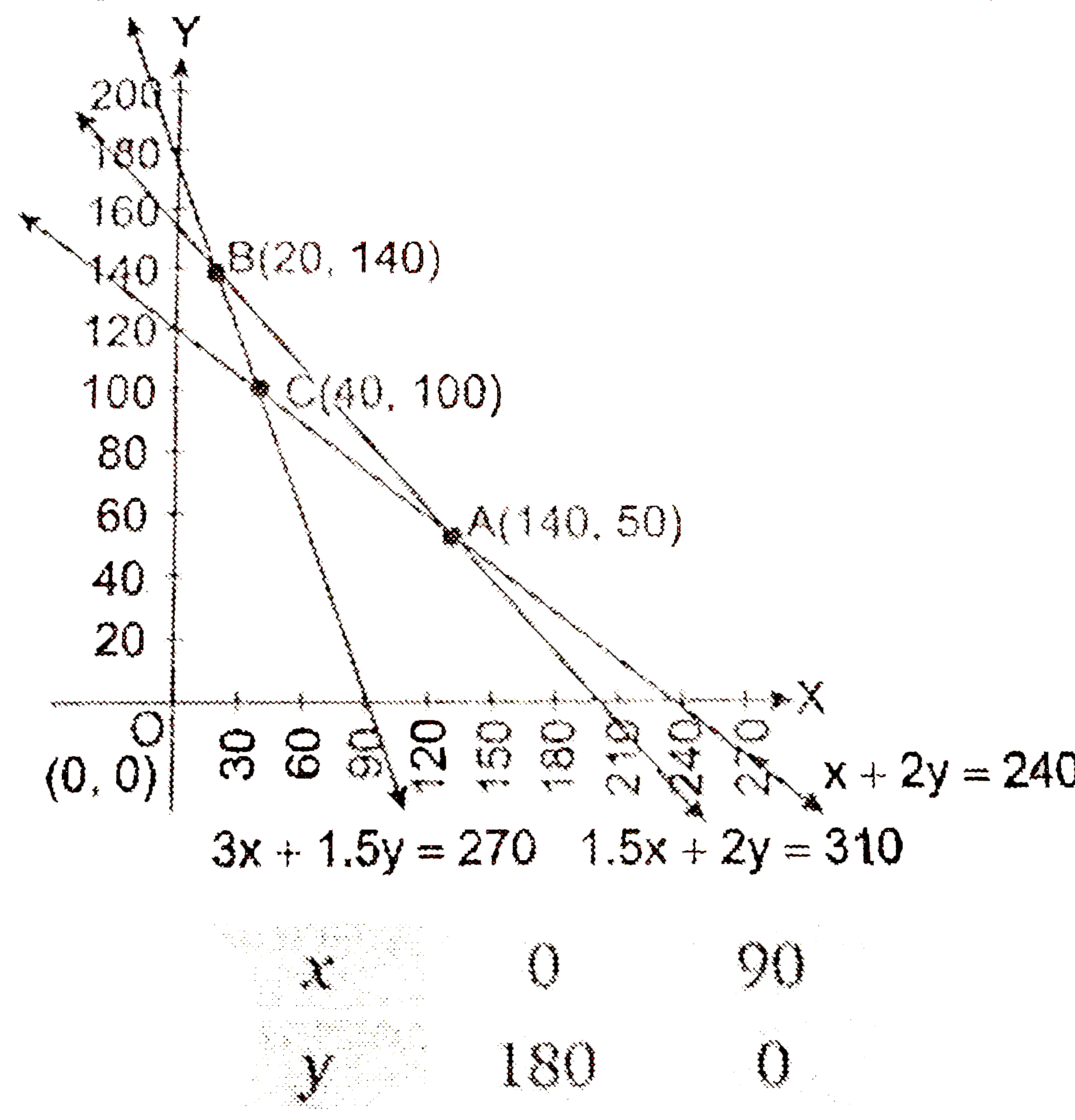Put `(0,0)` in the inequations `3x+1.5yge270` `3xx0+1.5xx0ge270implies0ge270` (False) Thus, the half plane does not contain origin. Now, draw the graph of the line `1.5x+2y=310` 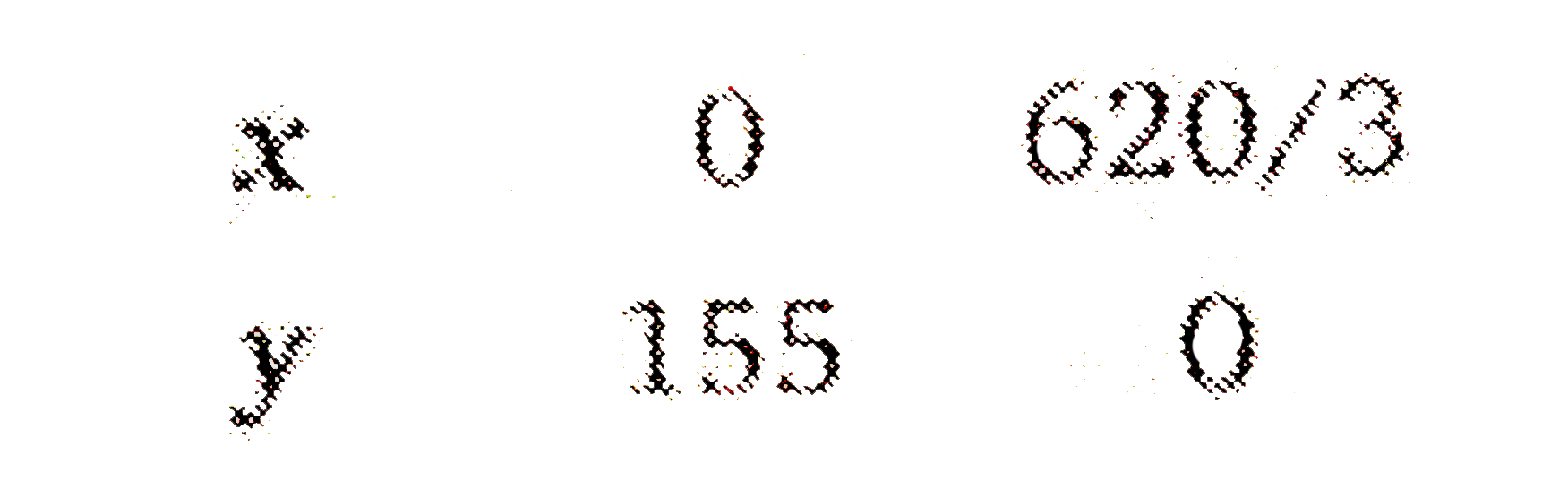PUt `(0,0)` in theinequation `1.5x+2yle310` `1.5xx0+2xx0le310implies0le310` (True) Thus, the half plane does not contain origin. Since `x,yge0` So the feasible region will be in first quadrant. The point of intersection of equations `1.5x+2y=310` and `x+2y=240` is `A(140,50)`. Similarly the point of intersection of the equation `3x+1.5y=270` and `1.5x+2y=310` is `B(20,140)`. `:.` Feasible region is ABCA. It vertices are `A(140,50),B(20,140)` and `C(40,100)` at which we find the value of `Z`. Therefore, the minimum value of `Z` is 470 at point `C(40,100)`. Minimum nitrogen to be MIXED in GARDEN is 470 kg for which 40 bags of brand `P` and 100 bats of brand `Q` should be used.

Discussion

No Comment Found

Related InterviewSolutions

P (-2,-1) and (0,-3) are the limiting points of a coaxial system of whichC -= x^(2) + y^(2)+ 5x + y + 4 = 0is a member. The circleS -= x^(2) + y^(2) - 4x - 2y - 15 = 0is orthogonal to the circle C . The point where the polar of P cuts the circle S is
Which of the following is/are discontinous at x = 1 ?
Write Minors and Cofactors of the elments of following determinants : |{:(1,0,4),(3,5,-1),(0,1,2):}|
The vertex of the parabola (y-1)^2 =8 (x-1) is at the centre of a circle and the parabola cuts that circle atthe ends of its latusrectum. Then the equation of that circle is
{{:(5x-3y=10),(6y=kx-42):} In the system of linear equations above, k represents a constant. If the system of equations has no solution, what is the value of 2k?
f(x) ={{:(1-sqrt(1-x^(2)),if -1lexle1),(1+ log ""(1)/(x), if xgt1):}
Given that alpha, beta, gamma, delta are in a geometric progression. If alpha, beta are the roots of x^(2)-x+p=0 " and "gamma, delta are the roots of x^(2)-4x+q=0, where p and q are integers, then the ordered pair (p, q) =
A poor , frustrated artist named Fresco created a plan to make money. He collected trash, repurposed it into sculptures, then asked various celebrities to write and paint on these trash objects, which he then sold on his own as modern high art. The chart below separately showsthe cost and revenue of his plan. The linear cost function, C(x) , represents the total money spent to make and market the art , while the linear revenue function, R(x) , shows the amount of money he has made in sculpture sales. Fresco initially spent money promoting the project in the media . He also had to pay the celebrities to participate . After 6 months , Fresco had created and sold x number of trash sculptures and finally broke even : he hadn't made or lost any money . How many sculptures did Fresco sell in his first 6 months of the project ?
A poor , frustrated artist named Fresco created a plan to make money. He collected trash, repurposed it into sculptures, then asked various celebrities to write and paint on these trash objects, which he then sold on his own as modern high art. The chart below separately showsthe cost and revenue of his plan. The linear cost function, C(x) , represents the total money spent to make and market the art , while the linear revenue function, R(x) , shows the amount of money he has made in sculpture sales. The cost function in the chart is determined by a constant production cost per sculpture - in this case, the amount Fresco pays each celebrity to participate - as well as a fixed cost , or the initial cost of promoting the project . What is the fixed cost of Fresco's trash sculpture project ?
An ellipse is incribed in a rectangle and if the angle between the diagonals is tan ^(-1)2sqrt2then e=

Discussion

No Comment Found

Related InterviewSolutions

Reply to Comment