Saved Bookmarks
| 1. |
A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical A small block kept in the bowl rotates with the bowl without slipping on its surface If the surface of bowl is smooth and angle made by radius through the block with the vertical is 0 find the angular speed at which the bowl is rotating . |
|
Answer» Solution :Here ` OA = R, ANGLEAOC = theta` Block moves in a horizontal circle with centre`C` and radius` r = AC = R sin theta` `:.` In equilibrium `N cos theta = MG` and `N sin theta = m OMEGA^(2) (R sin theta)` `N = m omega^(2) R` From(i)`m omega^(2) R cos theta = mg` ` omega = sqrt((g)/(R cos theta))` 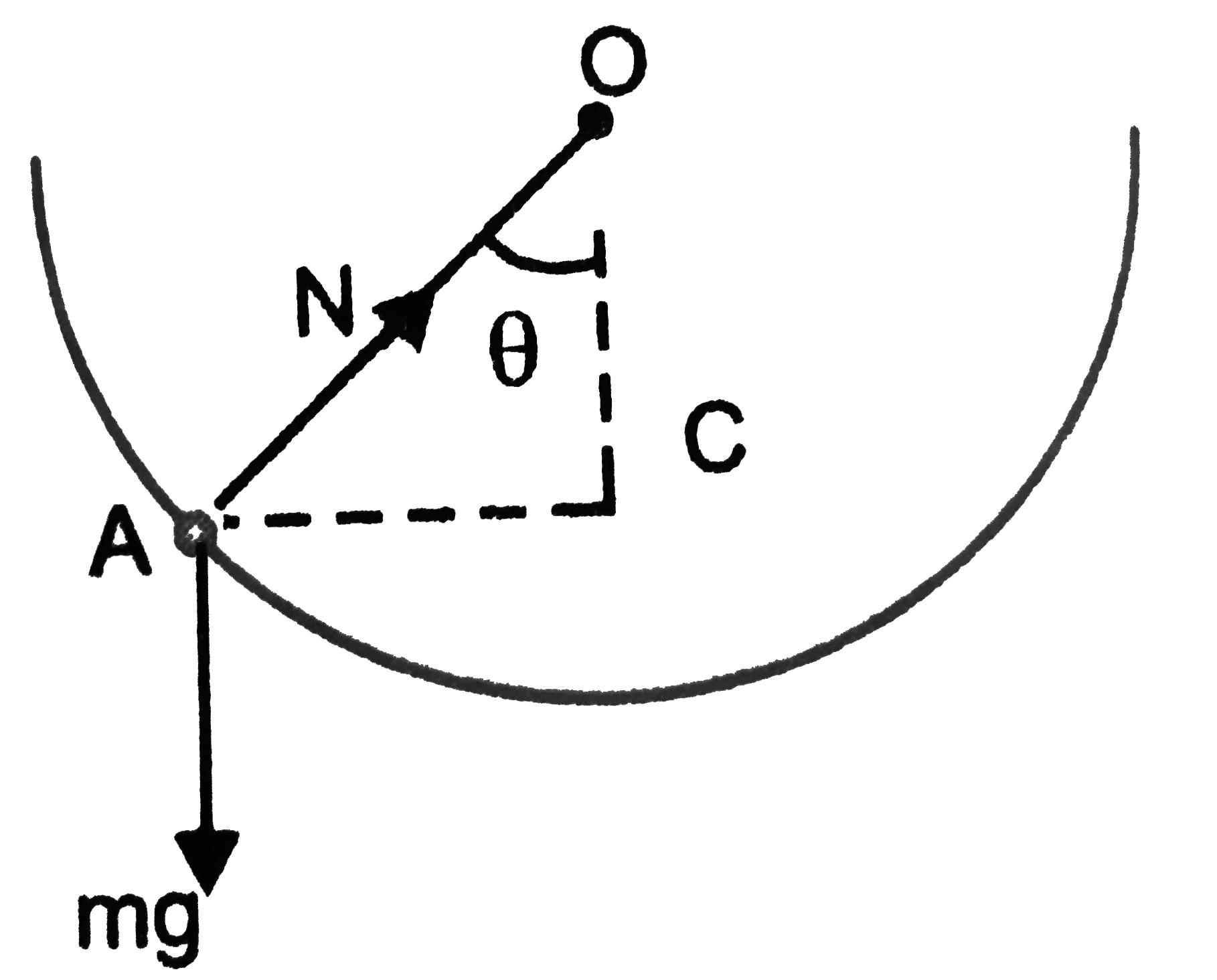 . .
|
|
Discussion
No Comment Found
Related InterviewSolutions
- What is uniform velocity
- Derive the speed time equation by calculas method
- 9×2y - 24x^2 +16y^3.factorise?
- Give me tips for preparation of physics??
- Advantage of friction
- Derivation of equation of Newton\'s Second Law of Motion that is F=ma
- Equation of projectile?
- Unit of Permeability
- Difference between vectr and scalar
- what is centripetal force ?