InterviewSolution
Saved Bookmarks
| 1. |
A manufacture produces two models of bike model X and model Y. Model X takes a 6 man hours to make per unit, while model Y takes 10 man hours per unit. There is a total of 450 man hour availbale per week. Handling and marketing costs are 2000 and 1000 per unit of model X and Y, respectively. The tota funds available for these purposes are 8000 per week. Profits per unit for models X and Y are 1000 and manufacturer produce, so, as to yeild a maximum profit? Find the maximum profit. |
|
Answer» `therefore 6x+10y le 450` `Rightarrow3x+5y le 225....(i) ` For models X and Y, handling and marketing costs are 2000 and 1000 respectively, total FUNDS available for these purposes are 80000 per week. `therefore 2000x+1000y ge 80000` `Rightarrow 2x+y ge 80` Also, `x ge 0, y ge....(ii)` Hence the profits per unit fo r models X and Y are 1000 and 500 respectively`therefore "Required LPP i"` Maximise Z=1000x+500y Subject to `3x+5y le 225, 2x+y le 80, x ge 0, y ge 0` From the shaded feasible region, it is clear that COORDINATES of corner points are (0,) (40,0),(25,30) and (0,45) On solving 3x+5y=225 and 2x+y=80, we get x=25, y=30 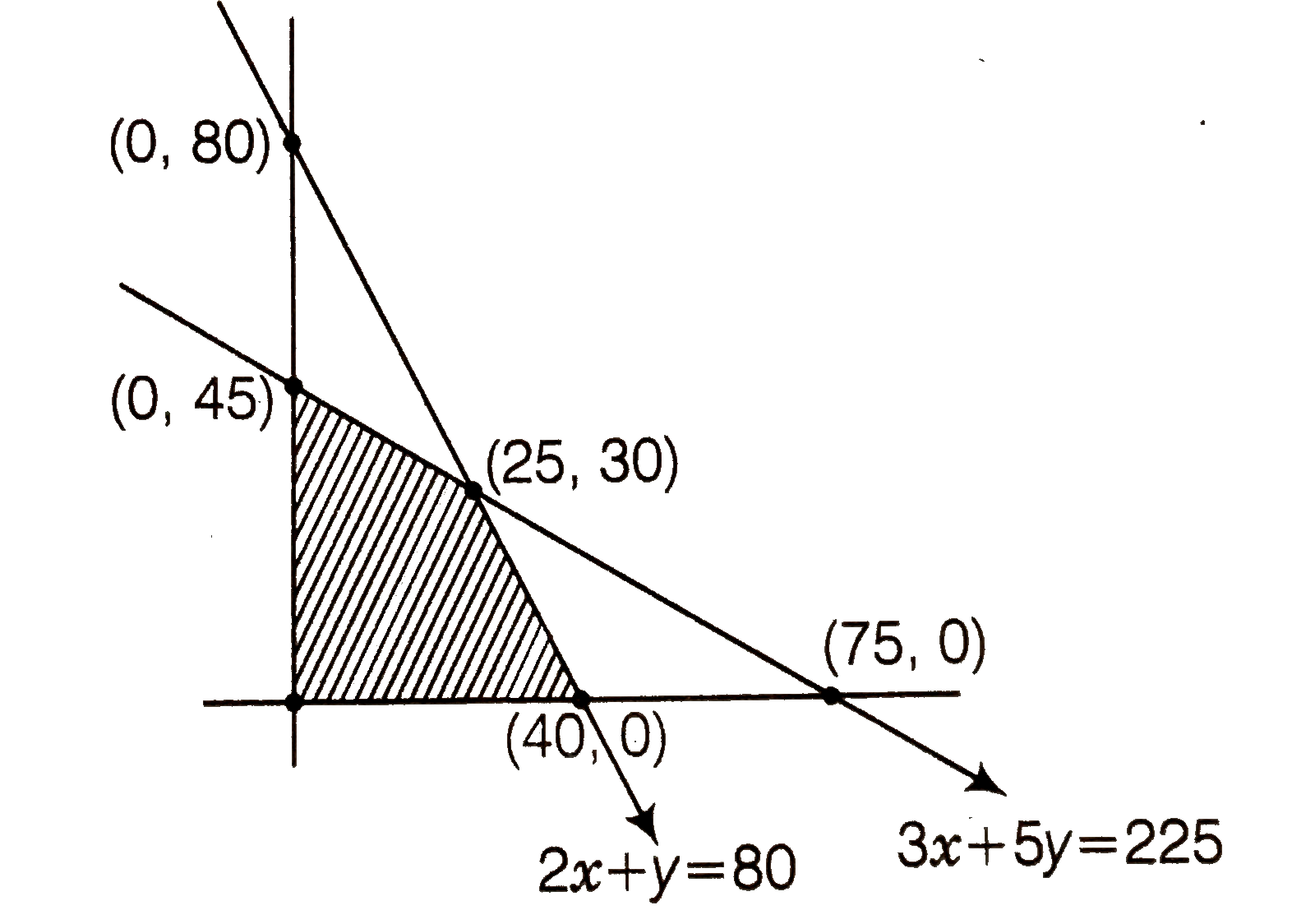 So, the manufacturer should poroduce 25 bikes of model X and 30 bikes of model Y to get a maximum PROFIT of 40000. Since in question it is asked that each model bikes should be produced. |
|