InterviewSolution
Saved Bookmarks
| 1. |
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day? |
Answer» Solution :Let the manufacturer produces `x` packets of nuts and `y` packets of bolts, then 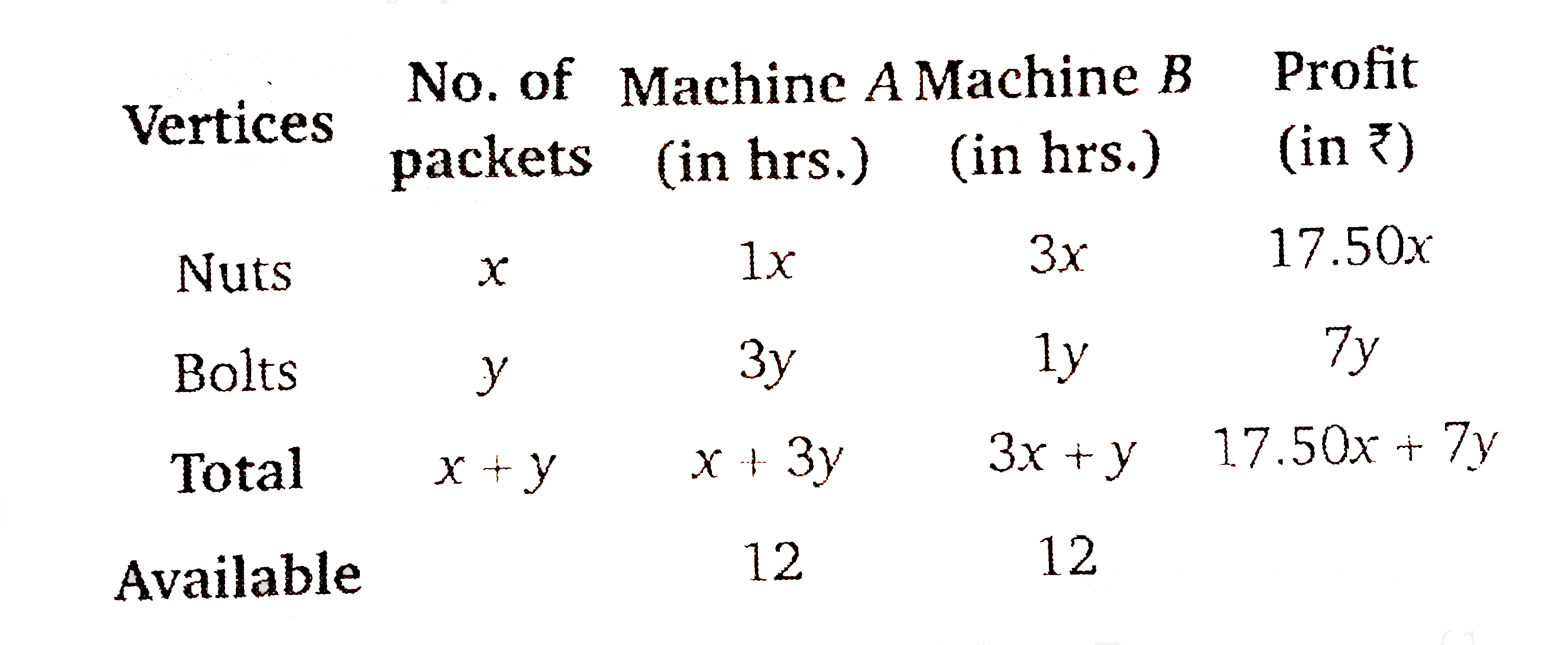 `:.` Maximise `Z=17.5x+7y`……………….1 and constraints `x+3yle12`………………………2 `3x+yle12`………………….3 `xge0,yge0`………………...4  First draw the graph of the line `x+3y=12`. 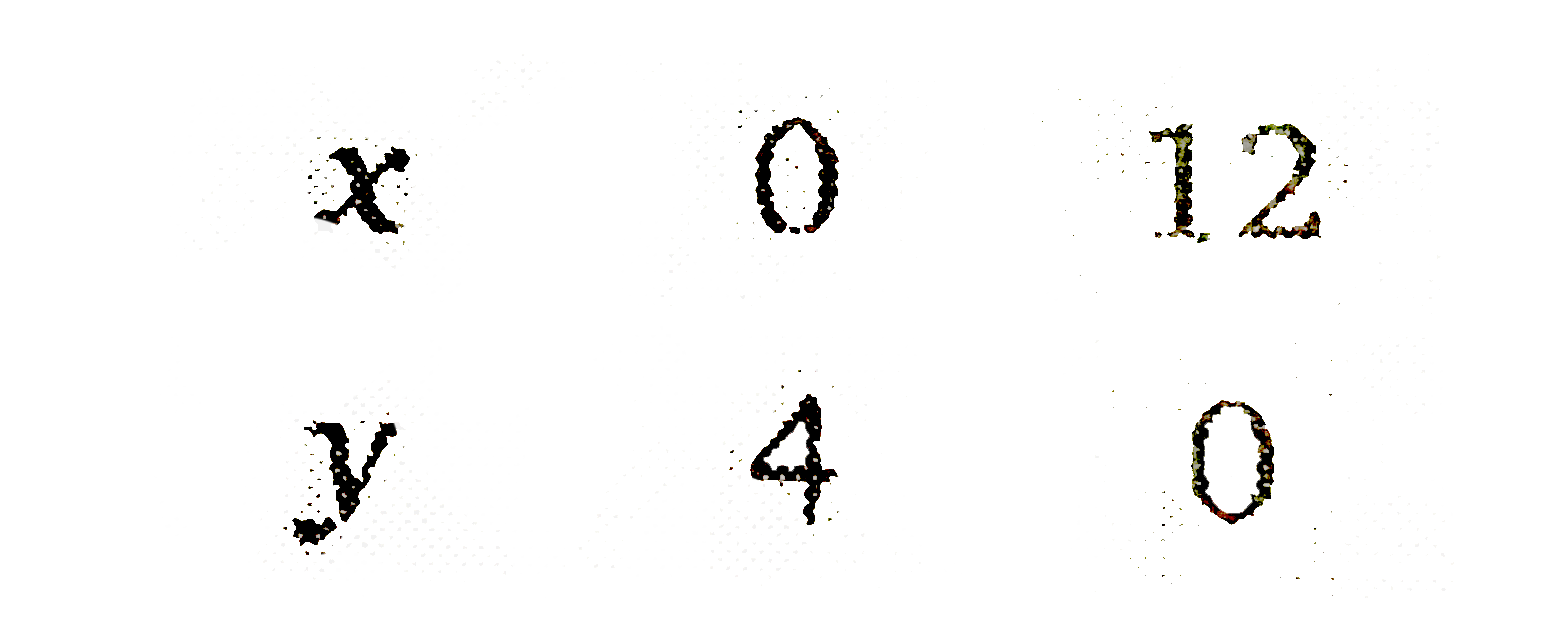 Put `(0,0)` in the inequation `x+3yge12` , `0+3xx0le10implies0le12` (True) Therefore half PLANE contains the origin. Since `x,yge0`. So the feasible region is in first quadrant, Now draw the graph of the line `3x+y=12` 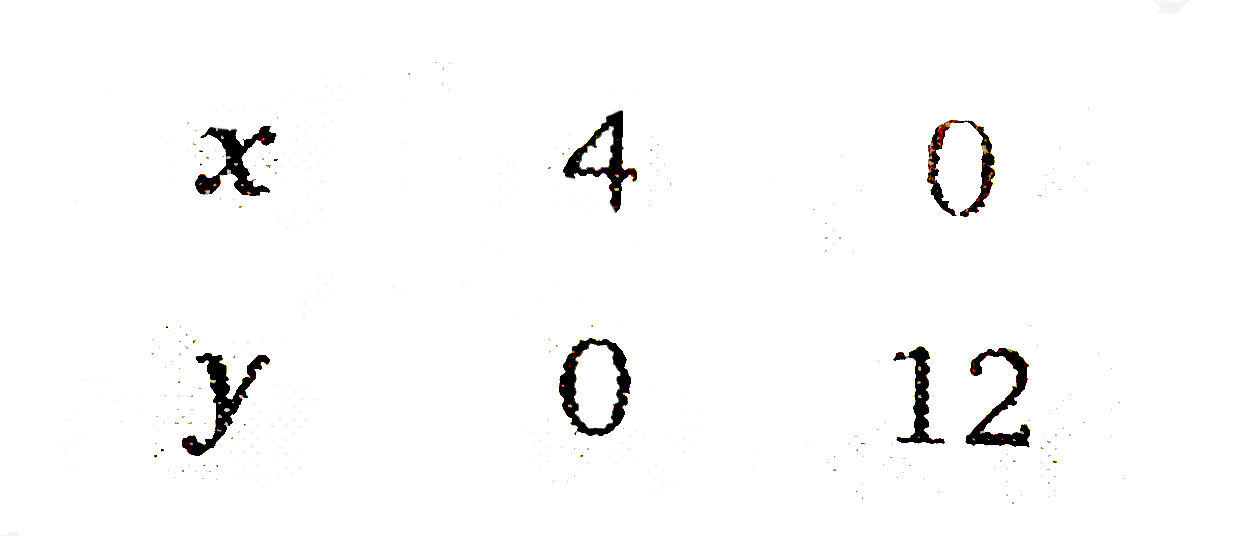 Put `(0,0)` in the inequation `3x+yle12`, `3xx0+0le12gt0le12` (True) Therefore, the half plane contains the origin. From the equations `x+3y=12` and `3x+y=12`, the point of INTERSECTION is `B(3,3)`. `:.` The feasible region is OABCO whose VERTICES are `O(0,0),A(4,0),B(3,3)` and `C(0,4)`. Now, we find the value of `Z` at these points, 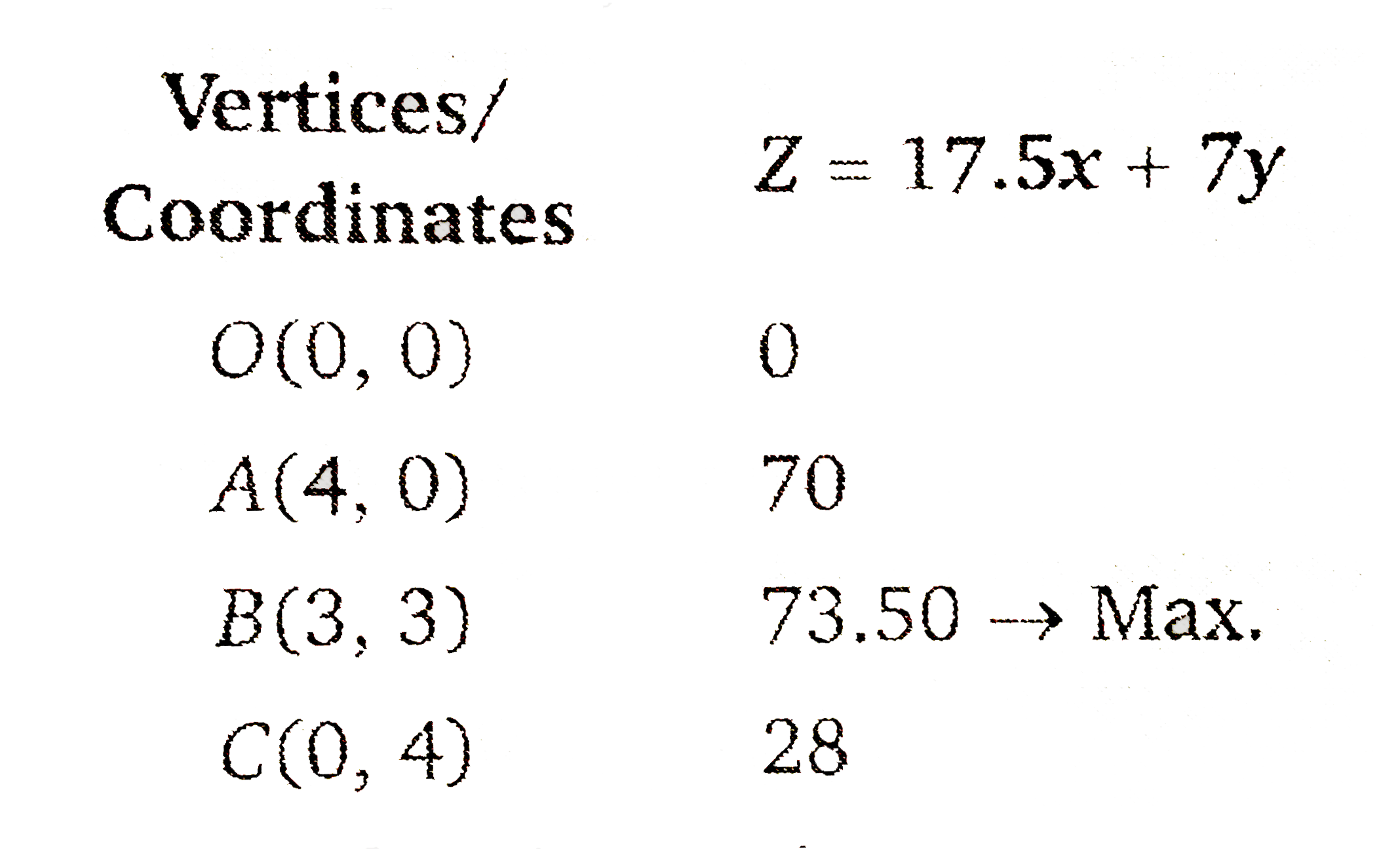 The value of `Z` is maximum Rs. 73.50 at point `(3,3)`. Therefore, the maximum profit of Rs. 73.50 can be obtained when 3 packets of nuts and 3 packets of bolts are produced PER DAY. |
|