1.

A particle (A) of mass m_(1) elastically collides with another stationary particle (B) of mass m_(2). Then :

Answer» <html><body><p>`(m_(1))/(m_(2)) = (1)/(2)` and the particles fly a part in the opposite direction with equal velocities.<br/>`(m_(1))/(m_(2)) = (1)/(3)` and the particles fly apart in the opposite direction with equal velocities.<br/>`(m_(1))/(m_(2)) = (2)/(1)` and the collision angle between the particles is `60^(@)` symmetrically.<br/>`(m_(1))/(m_(2)) = (2)/(1)` and the particles fly apart symmetrically at an angle `90^(@)`</p><a href="https://interviewquestions.tuteehub.com/tag/solution-25781" style="font-weight:bold;" target="_blank" title="Click to know more about SOLUTION">SOLUTION</a> :`m_(1)<a href="https://interviewquestions.tuteehub.com/tag/u-1435036" style="font-weight:bold;" target="_blank" title="Click to know more about U">U</a> + 0 = -m_(1)v+m_(2)v`……….(1) <br/> From kinetic <a href="https://interviewquestions.tuteehub.com/tag/energy-15288" style="font-weight:bold;" target="_blank" title="Click to know more about ENERGY">ENERGY</a> <a href="https://interviewquestions.tuteehub.com/tag/conservation-929810" style="font-weight:bold;" target="_blank" title="Click to know more about CONSERVATION">CONSERVATION</a> <br/> `(1)/(2)m_(1)u^(2) = (1)/(2)m_(1)v^(2) + (1)/(2)m_(2)v^(2)`………..(2) 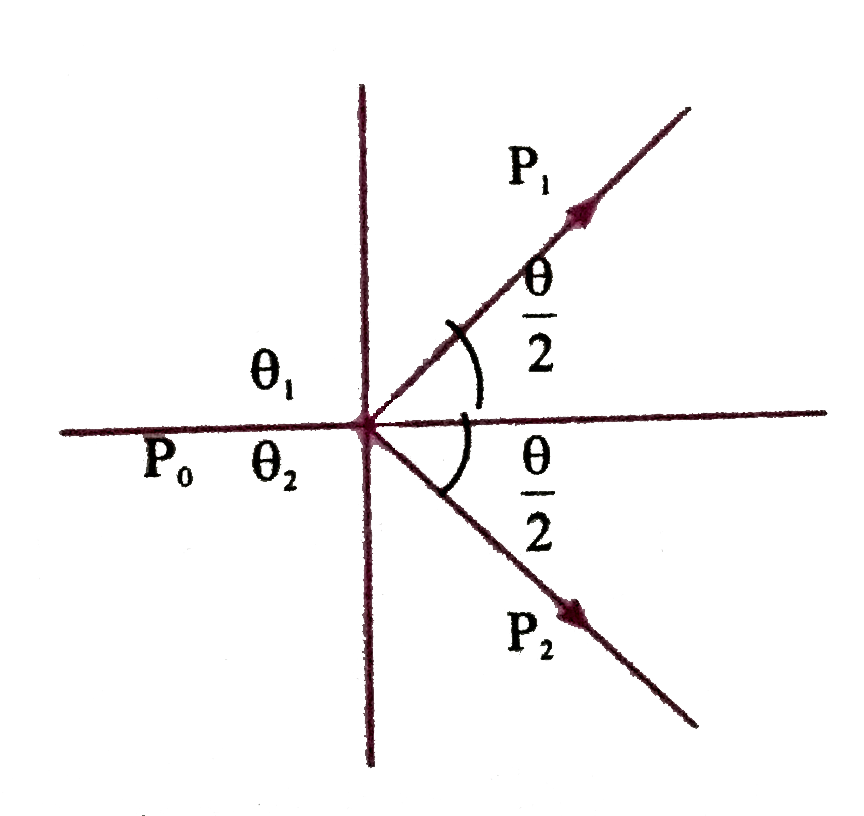<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NAR_PHY_XI_V02_C05_E01_050_S01.png" width="80%"/> <br/> From eq. (1) and and eq. (2) we get , `(m_(1))/(m_(2)) = (1)/(3)` <br/> So, choice (b) is correct. <br/> `P^(2) = P_(1)^(2) + P_(2)^(2)+2P_(1)P_(2) <a href="https://interviewquestions.tuteehub.com/tag/cos-935872" style="font-weight:bold;" target="_blank" title="Click to know more about COS">COS</a> theta`.........(1) <br/> Also from conservation of kinetic energy <br/> `(P^(2))/(2m_(1)) = (P_(1)^(2))/(2m_(1)) + (P_(2)^(2))/(2m_(2))`............(2) <br/> Since particles fly symmetrically <br/> `P_(1) sin "(theta)/(2) = P_(2) sin "(theta)/(2)`..........(3) <br/> Solving eq. (1), (2) and (3) we get <br/> `(m_(1))/(m_(2)) = (2)/(1)`</body></html>


Discussion

No Comment Found

Related InterviewSolutions