InterviewSolution
Saved Bookmarks
| 1. |
A particle P moves on the line y=x, xle0 with constant speed u m//sec. Another particle Q revolves along the circke (x-1)^(2)+y^(2)=1/9 with constant speed (omega)/3m//sec. In anticlockwise directio, let at t=0, both P and Q simultaeously started, P from the point (0,0) and Q from he point (2/3,0). Further at any time instant t sec, let the distance of theri separation is r(t)m. Also it was observed that at time t_(0) sec, both P and Q are at their closest distance of approach, denoted by r_("minimum")m, then choose the correct statements from among the following |
|
Answer» <P>`[12r_("minimum")]=4` (where [.] denotes the greatest integer function) `y=-x+1,(x-1)^(2)+y^(2)=1/3` `x+y-1=0,2y^(2)=1/9` `x-1=y,y^(2)=1/(3sqrt(2))` 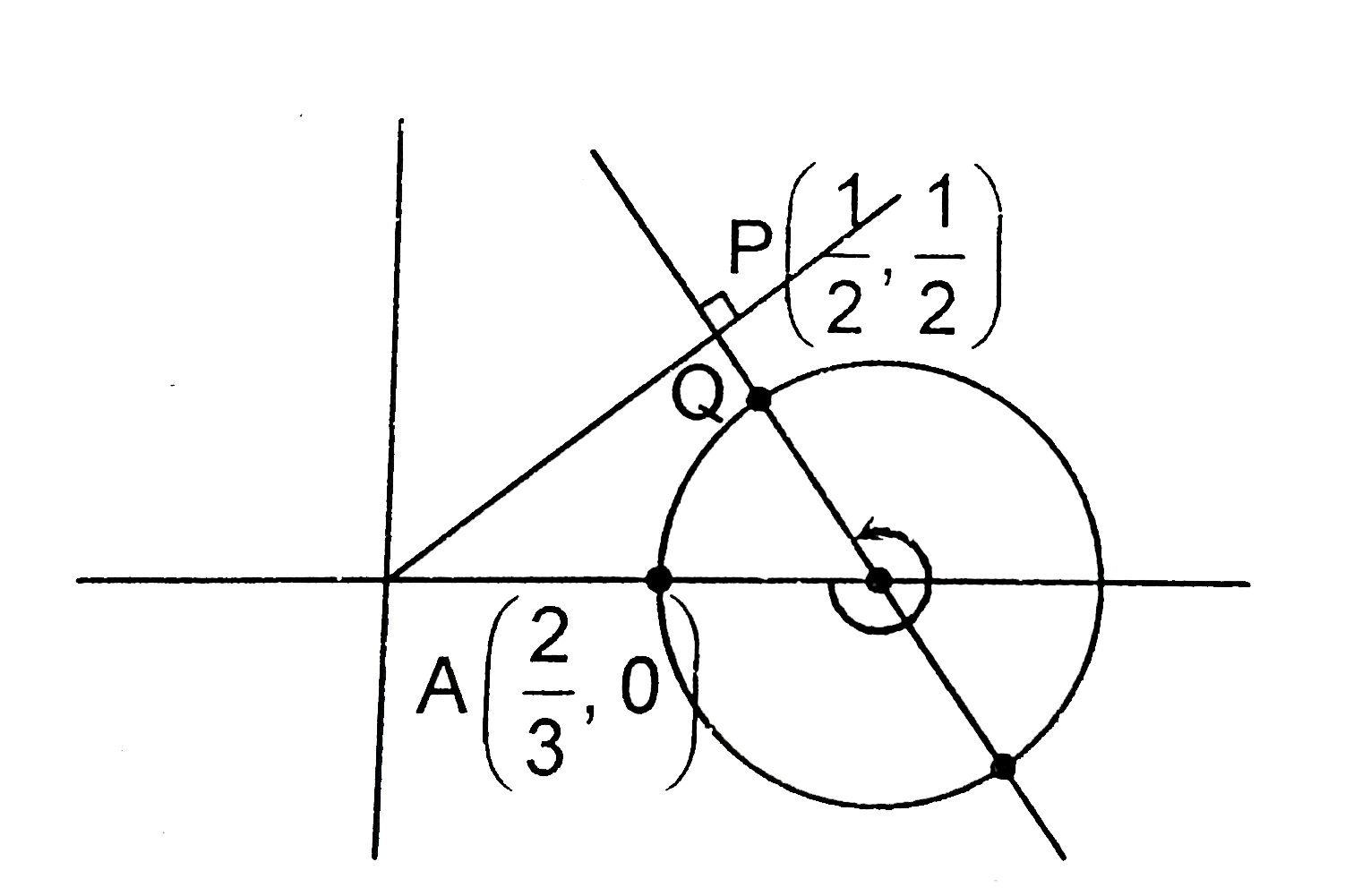 Clearly SHORTEST distance of approach is along common normal whose equation is `x+y=1=0`. So, when they are at their CLOSEST distance `P` must be at `(1/2,1/2)` and `Q` must be at `(1- 1/(3sqrt(2)),1/(3sqrt(2)))` covering angle `(7pi)/4` on the circle . Since `P` and `Q` happened to be at these points at same time so we have `t_(0)=(7pi)/(4w)=1/(sqrt(2u))` also at this instance `t_(0),r_("min")=(3-sqrt(2))/(3sqrt(2))IMPLIES[12r_("min")]=[6sqrt(2)-4]=4` Also at any time instant `t_(1)` co-ordinate of `P,Q` are `((ut)/(sqrt(2)),(ut)/(sqrt(2)))` at `Q(1+(cos(omegat))/3,+sin((omegat)/3))` `:.r^(2)(t)=((ut)/(sqrt(2))-1 - (cos(omegat))/3)^(2)+((ut)/(sqrt(2))-(sin(omegat))/3)^(2)` |
|