InterviewSolution
Saved Bookmarks
| 1. |
A rectangle HOMF has sides HO=11 and OM=5. A triangle ABC has H as the intersection of the altitude, O the centre of the circumscribed circle M the mid point of BC, and F the foot of the altitude from A, then |
|
Answer» perimeter of `DeltaABC`is greater than 70 Since `/_HFB=/_AFC, /_HBF=/_ACF` So `,DeltaBFH` and `DeltaAFC` are similar `(BF)/(HF)=(AF)/(FC)impliesBF.FC=FA.HF=75` Now `BC^(2)=(BF+CF)^(2)=(BF-CF)^(2)+4BF.FC` But `FC-BF=(FM+MC)-(BM-FM)=2FM=22` `BC=sqrt(22^(2)+4xx75)=28` 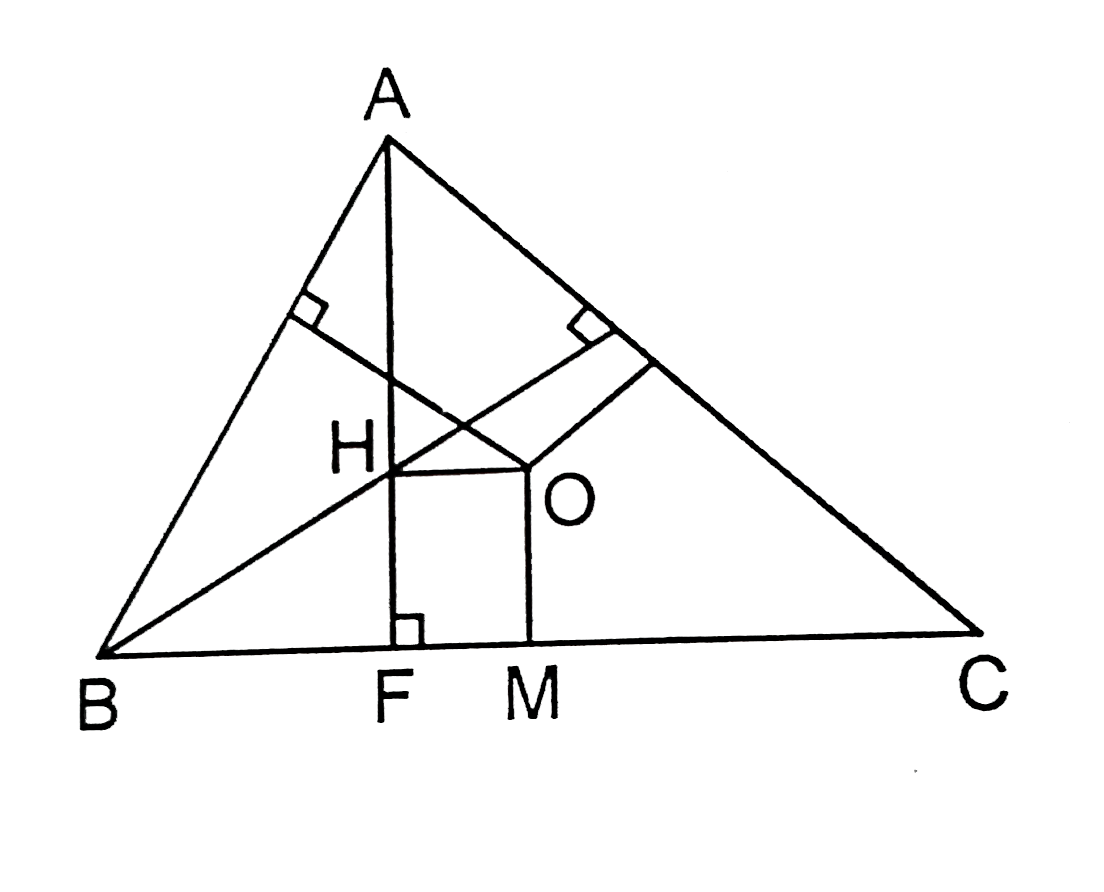
|
|