1.

A slightly loose fit widnow is balanced by two strings which are connected to weights w//2 each. The stringes pass over the frictionless pulleys as shown in the figure. The stringes are tied almost at the corner of the window accelerates downward. If coefficient of friction between the window and the side supports is mu then calculate the acceleration of the window in terms of mu, a, b and g. whereas width and b is the lengths of he window. .

Answer» <html><body><p><br/></p>Solution :Translational motion of window <br/> `w - T - 2f = (w)/(<a href="https://interviewquestions.tuteehub.com/tag/g-1003017" style="font-weight:bold;" target="_blank" title="Click to know more about G">G</a>) A` <br/> `w - T - 2 mu N = (w)/(g) A`…(1) <br/> Translational motion of weight <br/> `T - (w)/(2) = (w)/(2 g) A rArr T = (w)/(2) (1 + (A)/(g))` ….(2) <br/> <a href="https://interviewquestions.tuteehub.com/tag/taking-1238585" style="font-weight:bold;" target="_blank" title="Click to know more about TAKING">TAKING</a> torque about `C.M` 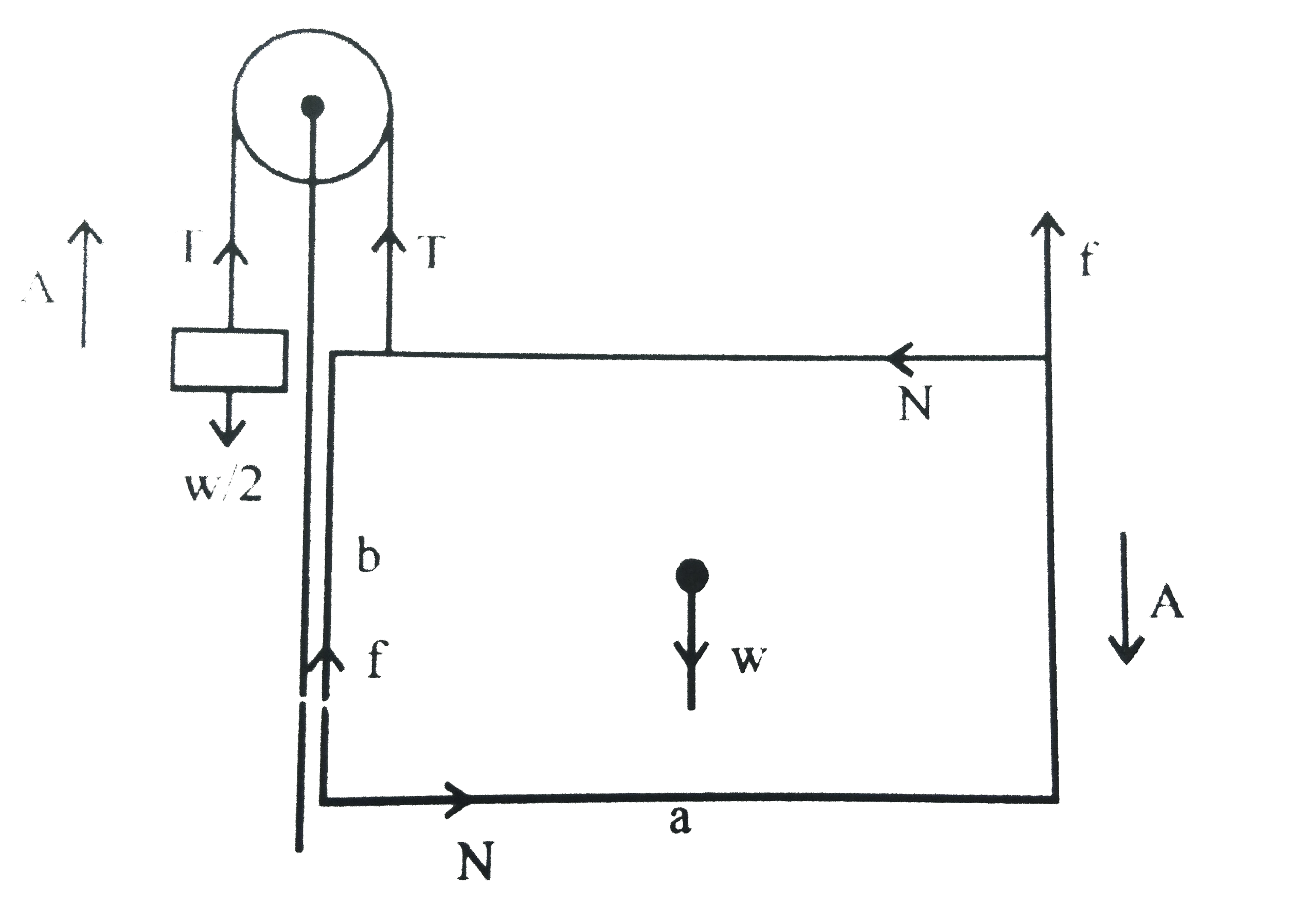<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_MEC_V01_C03_E01_153_S01.png" width="80%"/> <br/> `<a href="https://interviewquestions.tuteehub.com/tag/f-455800" style="font-weight:bold;" target="_blank" title="Click to know more about F">F</a> xx (a)/(2) + T xx(a)/(2) -<a href="https://interviewquestions.tuteehub.com/tag/2n-300431" style="font-weight:bold;" target="_blank" title="Click to know more about 2N">2N</a> xx (b)/(2) -<a href="https://interviewquestions.tuteehub.com/tag/fxx-1002989" style="font-weight:bold;" target="_blank" title="Click to know more about FXX">FXX</a>(a)/(2) = 0` <br/> `T = 2N (b)/(a)`...(3)<br/> From (2) and (3) <br/> `(w)/(2) ((g + A))/(g) = (2Nb)/(a)` <br/> `N = (wa(g+A))/(4 bg)`...(4) <br/> From (1),(2) and (4) <br/> `w -(w)/(2) ((g+A))/(g) - (2 mu wa(g +A))/(4 bg) = (w)/(g) A` <br/> `1-(1)/(2) ((g-A))/(g) - ((2mu ag +A))/(4bg) = (A)/(g)` <br/> `1 -(1)/(2) -(mu a)/(2b) = (A)/(g) + (A)/(2g) + (mu aA)/(2 bg)`<br/> `((b - mua))/(2b) = ((3b + mua)/(2bg)) A rArr A = ((b - mu a)g)/((3b + mu a))`.</body></html>


Discussion

No Comment Found

Related InterviewSolutions