InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
A tangent is drawn at any point on the hyperbola (x^(2))/(a^(2))-(y^(2))/(b^(2)) =1. If this tangent is intersected by the tangents at the vertices at points P and Q, then which of the following is/are true |
|
Answer» S,S',P and Q are concyclic 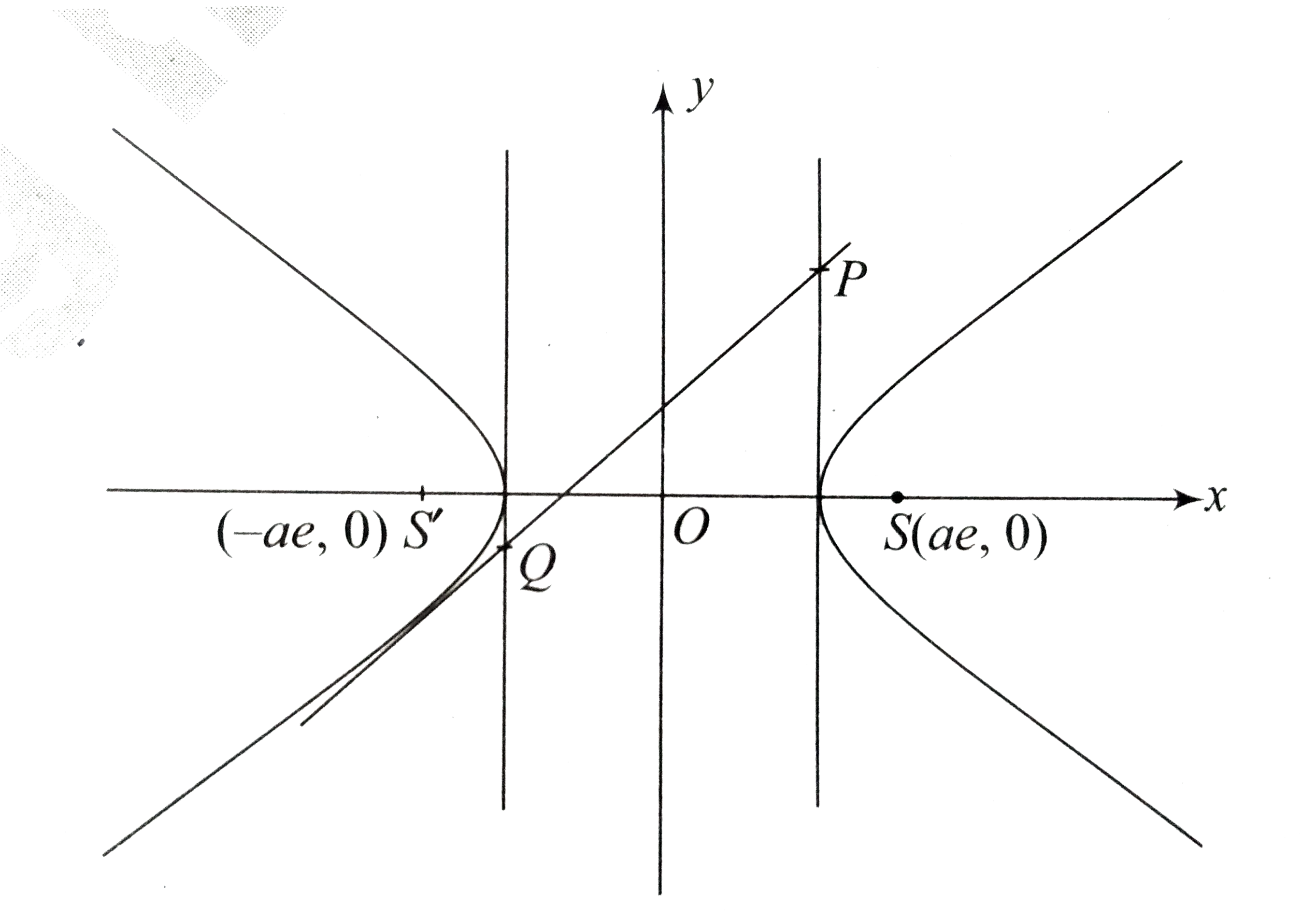 Any tangent to the hyperbola is `(X sec THETA)/(a) -(y TAN theta)/(b) =1` Solving this line with the lines `x = +-a`, we get the COORDINATES of points P and Q as `(a,b tan.(theta)/(2))` and `(-a,-b cot.(theta)/(2))` Now slopes of the lines PS and QS are `m_(PS) =(btan.(theta)/(2))/(a(1-e)), m_(QS) =(-b cot.(theta)/(2))/(-a(1+e))` `rArr m_(PS).m_(QS) =(-b^(2))/(a^(2)(e^(2)-1)) =-1` Similarly `m_(PS). m_(QS') =-1` `rArr` line PQ subtends and angle of `(pi)/(2)` at S and S' `rArr` points P,Q,S and S' are concyclic. `rArr PQ` is diameter. |
|