InterviewSolution
Saved Bookmarks
| 1. |
An ellipse is inscribed in a reactangle and the angle between the diagonals of the reactangle is tan^(-1)(2sqrt(2)), then find the ecentricity of the ellipse |
Answer» 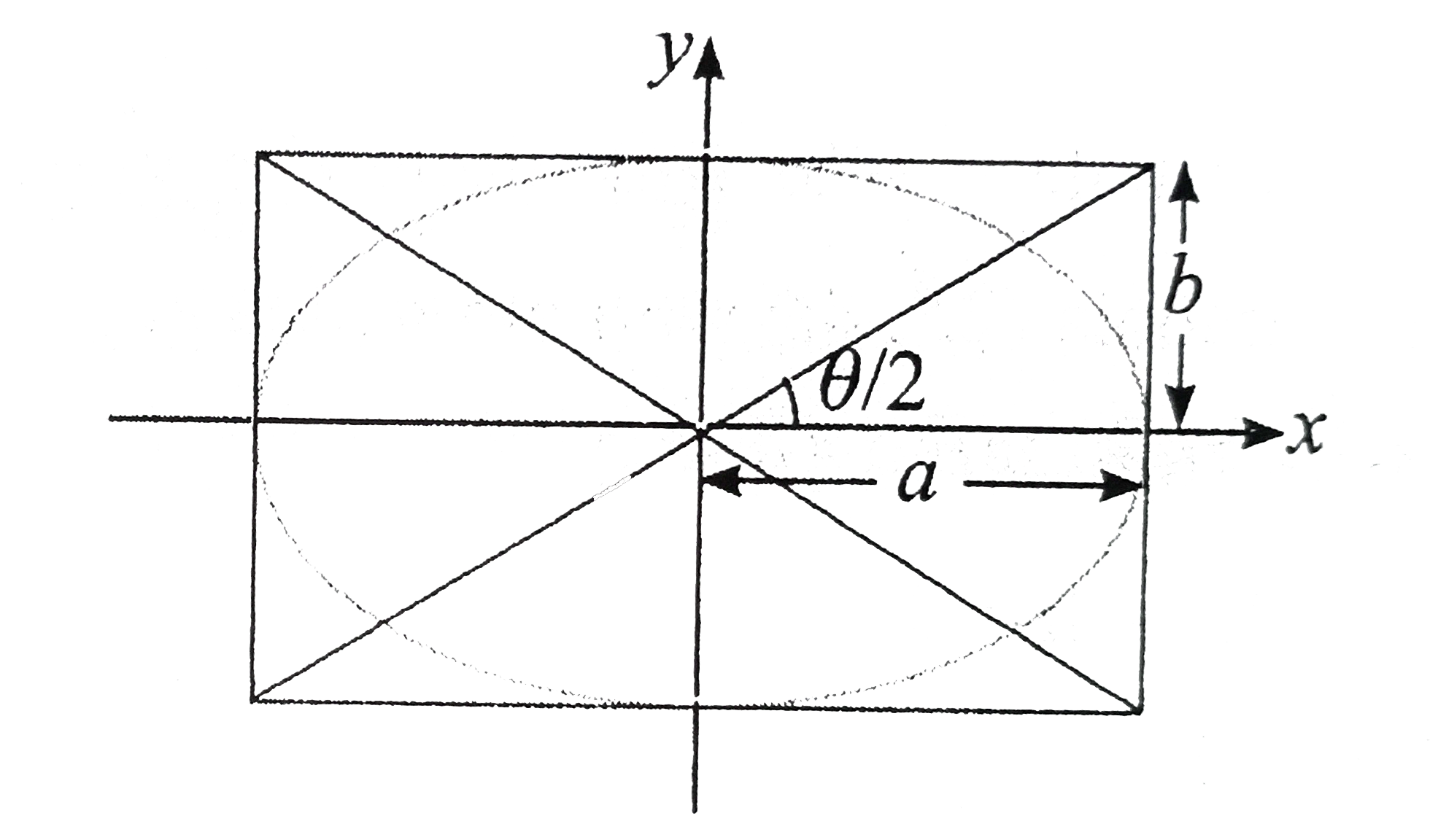 From the FIGURE, we have `TAN.(THETA)/(2)=(b)/(a)rArrtan^(2).(theta)/(2)=(b^(2))/(a^(2))` `rArr(1-costheta)/(1+cos theta)=(b^(2))/(a^(2))` `rArr(1-(1)/(3))/(1+(1)/(3))=(b^(2))/(a^(2))rArr(b^(2))/(a^(2))=(1)/(2)` `:. e=sqrt(1-(b^(2))/a^(2))=(1)/(sqrt(2))` |
|