InterviewSolution
Saved Bookmarks
| 1. |
Consider a DeltaABC in which sides AB and ACare perpendicular to x-y-4=0 and 2x-y-5=0, repectively. Vertex A is (-2, 3) and the circumcenter of DeltaABC is (3/2, 5/2). The equation of the line in List I is of the form ax+by+c=0, where a,b,c in I. Match it with the corresponding value of c in list II and then choose the correct code. Codes : {:(a, b, c, d),(r, s, p, q),(s, r, q, p),(q, p, s, r),(r, p, s, q):} |
Answer» 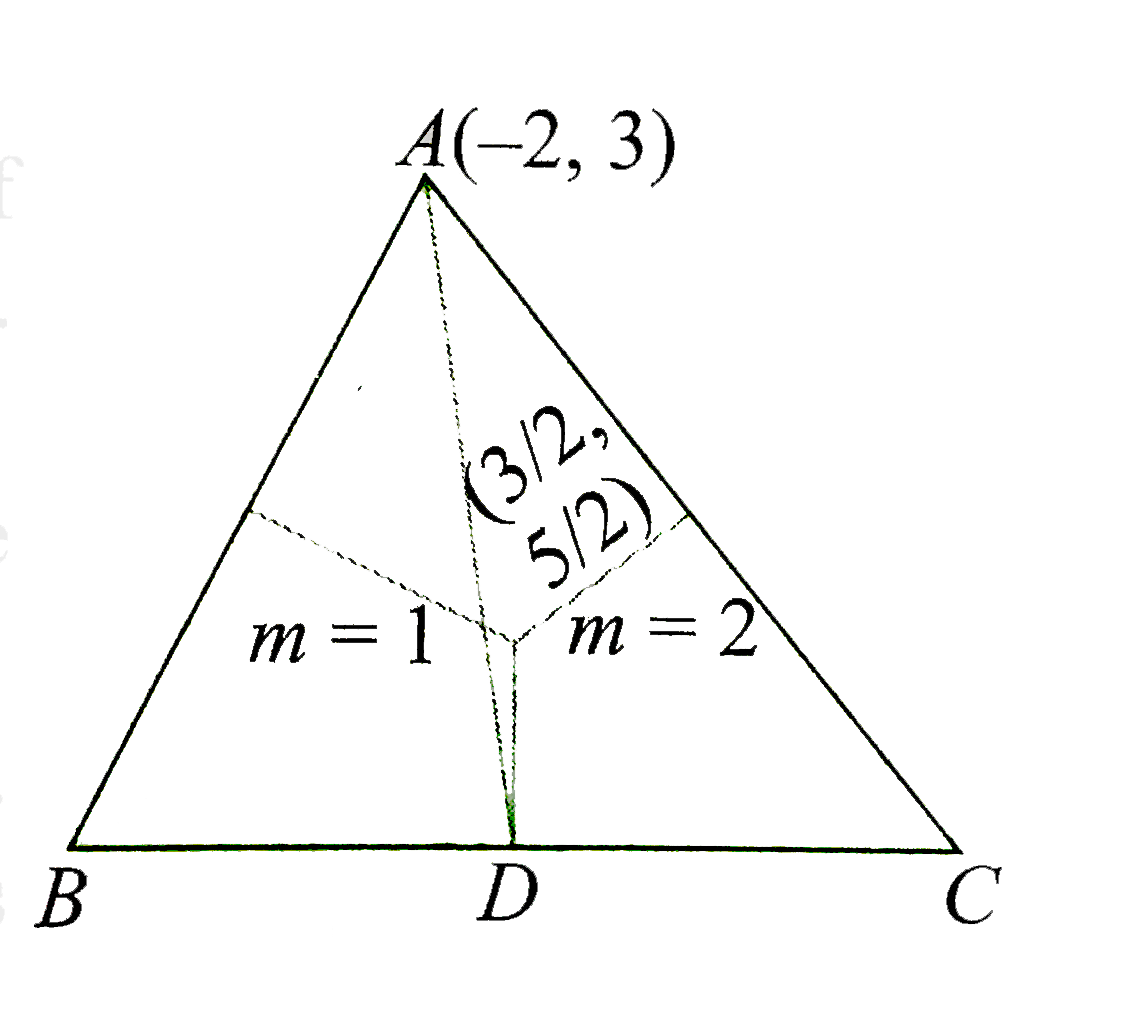 The perpendicular bisector of AB is parallel to x-y-4=0. THEREFORE, the slope is 1. It is passing through the circumcenter, i.e, (3/2, 5/2). Therefore, the line is x-y+1 =0. b. The perpendicular bisector of AC is B parallel to 2x-y-5=0. Therefore, the slope is 2. It is passing through the circumcenter, i.e., (3/2, 5/3). Therefore, the line is 4x-2y-1=0. c. The EQUATION of perpendicular bisector to AC is 2x-y-5=0. Therefore, the equation of AC can be`x+2y+lambda= 0.` It is passing through A(-2, 3). Therefore, `lambda = -4` Therefore, the equation of AC is x+2y-4=0. d. The image of A on the perpendicular bisector of AC is `(x+2)/(4) = (y-3)/(-2) = (-2(-8-6-1))/(16+4) = (3)/(2)` `therefore C-= (4, 0)` The image of A on the perpendicular bisector of AB is `(x+2)/(1) = (y-3)/(-1) = (-2(-2-3+1))/(1+1) = 4` Therefore, B is (2, -1). Therefore, the midpont of BC is D (3, -1/2). Hence, the median through A is 7x+10y-16=0. |
|