Consider a long steel bar under a tensile stress due to force F acting at the edges along the length of the bar (as shown in figure). Consider a plane making an angle with the length. What are the tensile and shearing stresses on this plane? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?

Consider a long steel bar under a tensile stress due to force F acting

1.	Consider a long steel bar under a tensile stress due to force F acting at the edges along the length of the bar (as shown in figure). Consider a plane making an angle with the length. What are the tensile and shearing stresses on this plane? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
Answer» Solution :THINK below figure, 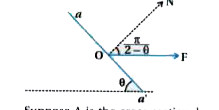Suppose A is the cross sectional area of the bar. Let for balance of pane aa. angle `pi/2 - theta` between perpendicular ON to the pane and FORCE F. The parallel component of force to the pane, `F_(P) = F sin ((pi)/(2) - theta) = F cos theta and ` Perpendicular component, `F_(N) = F cos ((pi)/(2) -theta)= F sin theta` Suppose A is area of pane (face) aa. `therefore (A)/(A.) = sin theta` `therefore A. = (A)/(sin theta )` Tensile stress `= ("perpendicular force")/("area") = (F _(N))/(A.)= (F sin thea)/(A//sin theta)` `therefore` Tensile stress `= F/A sin ^(2) theta ` (a) For MAXIMUM stress `F/A sin ^(2) theta ` should be maximum. `sin ^(2) theta =1` `therefore sin theta =1` `therefore theta = (pi)/(2)` For this `theta = 90^(@)` Shearing stress `= ("parallel force")/("area") = (F _(p ))/(A.)` ` = (F cos theta )/(A //sin theta) = F/A sin theta cos theta= (F)/(2A) xx sin 2 theta` `[ because 2 sin theta cos theta = sin 2 theta]` (b) For shearing stress to be maximum `sin 2 theta =1` `therefore 2 theta =90^(@)` `therefore theta = 45^(@)`