InterviewSolution
Saved Bookmarks
| 1. |
Consider the traingle having vertices O(0,0),A(2,0), and B(1,sqrt3). "Also" b le"min" {a_1,a_2,a_3....a_n} meansb le a_1 when a_1 is least, b le a_2 when a_2 is least, and so on. Form this, we can say b le a_1,b le a_2,.....b le a_n. Let R be the region consisting of all the those points P inside DeltaOAB which satisfy.OPle"min"[BP,AP]. Then the area of the region R is |
|
Answer» `SQRT(3)`sq,units 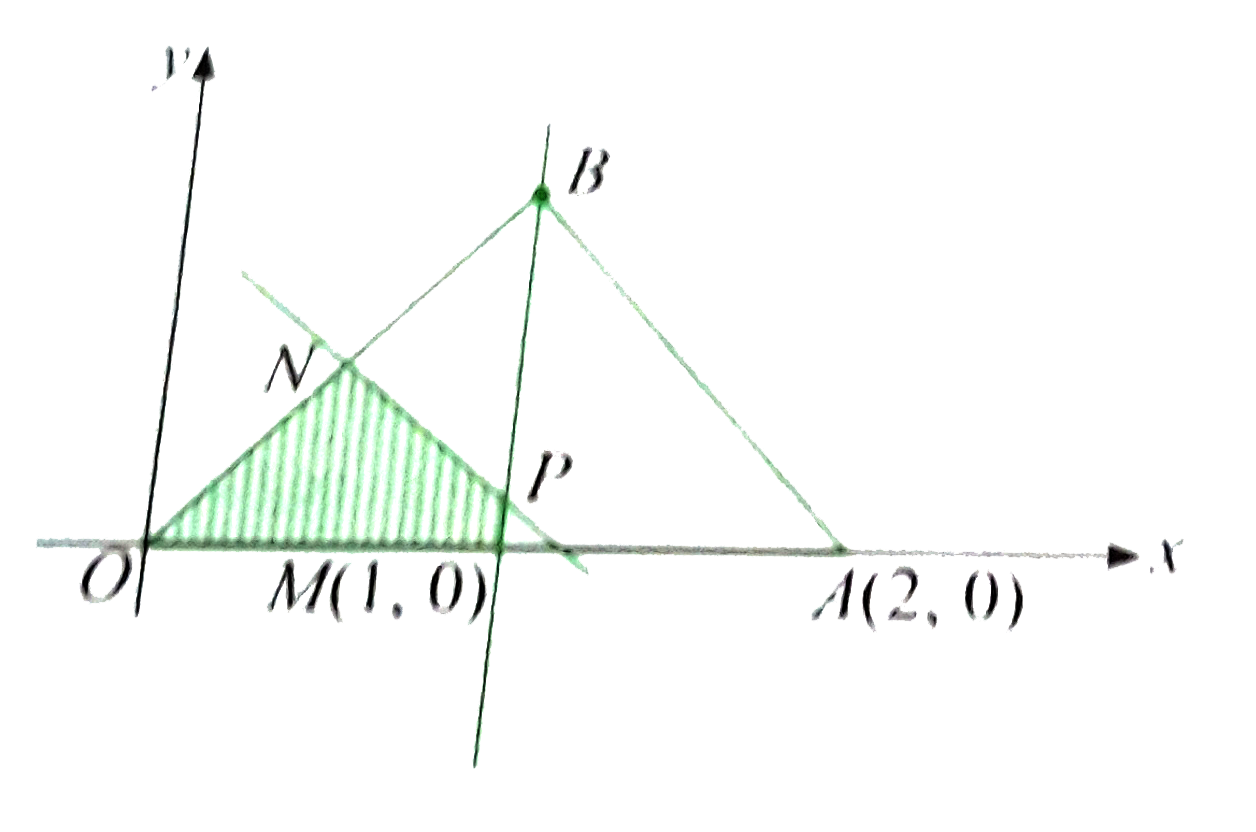 `OP le "min"[BP,AP]` `OP le AP(whenAPlt BP)` LET `OP=BP`. The P lies on the perpendicular bisector of OB, For `OP=AP,P` lies on the perpendiuclar bisector of OA. Then, for the required condition, P lies in the REGION as shown in the diagram. the AREA of region `OMPN` is `(1)/(2)xx|{:(0,,0,,),(1,,0,,),(1,,1//sqrt3,,),(1/2,,sqrt(3)//2,,),(0,,0,,):}|=(1)/(2)[(1)/(sqrt3)+(sqrt3)/(2)-(1)/(2sqrt3)]` `=(1)/(2)[sqrt(3)/(2)+(1)/(sqrt3)]=(1)/(sqrt3)` |
|