InterviewSolution
Saved Bookmarks
| 1. |
Consider two regions R_(1):"points P are nearer to (1,0) than to "x=-1. R_(2): "Points P are nearer to (0,0) than to (8,0)" Find the area of the region common to R_(1) and R_(2). |
|
Answer» <P> `therefore""sqrt((x-1)^(2)+y^(2))lt|x+1|` `rArr""y^(2)lt4x` `rArr"point P lie inside parabola "y^(2)=4x` `R_(2) :` Points P(x,y) are nearer to (0,0) than to (8,0) `therefore""|x|lt|x-8|` `rArr""x^(2)LTX^(2)-16x+64` `rArr""xlt4` `rArr""`point P lie to the left side of line x=4 The AREA of common region of `R_(1) and R_(2)` is area bounded by x=4 and `y^(2)=4x.` 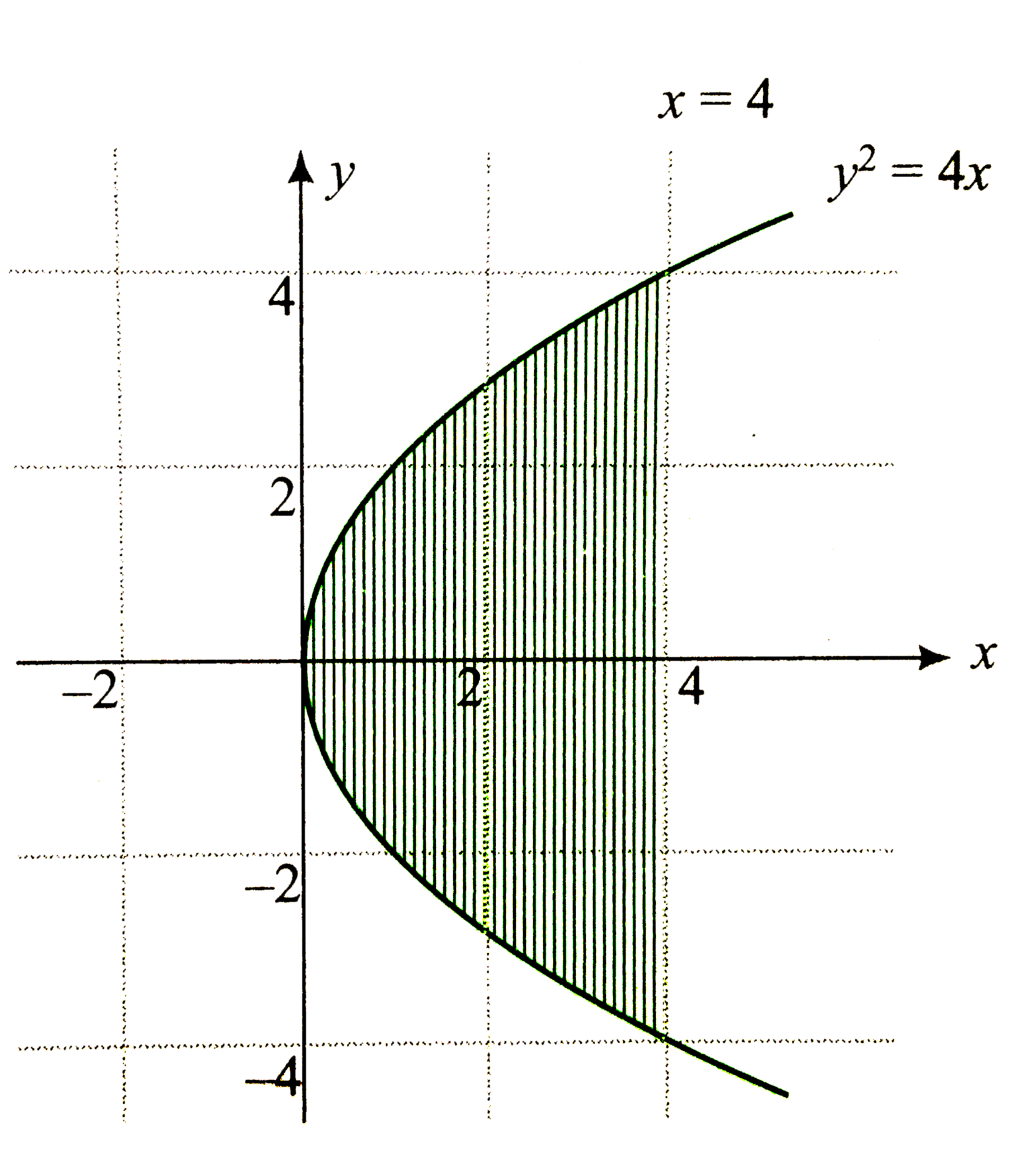 `therefore"Required area "=2overset(4)underset(0)int(4-(y^(2))/(4))dy` (Integrating along x-axis) `=2[4y-(y^(3))/(12)]_(0)^(4)` `=2[16-(64)/(12)]` `(64)/(3)` sq. units |
|