1.

Derive the expression for moment of inerita of a uniform disc about an axis passing through the centre and perpendicular to the plane.

Answer» <html><body><p></p>Solution :Let us consider a disc of mass M and radius R. It is found that thisdisc is made up of many infinitesimally small rings as shown in the figure. Consider <a href="https://interviewquestions.tuteehub.com/tag/one-585732" style="font-weight:bold;" target="_blank" title="Click to know more about ONE">ONE</a> such ring of mass (dm) and thickness (dr) and radius (r). The moment of inerita (dI) of this small ring isgiven by <br/> `dI=(dm)r^(2)` <br/> As the mass is uniformly distributed the mass per unit <a href="https://interviewquestions.tuteehub.com/tag/area-13372" style="font-weight:bold;" target="_blank" title="Click to know more about AREA">AREA</a> `(sigma)` is `sigma=("mass")/("area")=M/(piR^(2))` 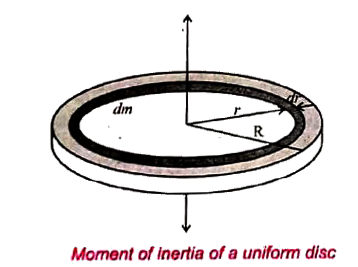<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PRE_GRG_PHY_XI_V02_C05_E01_036_S01.png" width="80%"/> <br/> The mass of the infinitesimaly small ring is given by <br/> `dm=sigma 2pirdr-M/(piR^(2)) <a href="https://interviewquestions.tuteehub.com/tag/2pi-1838601" style="font-weight:bold;" target="_blank" title="Click to know more about 2PI">2PI</a> r dr` <br/> where tehh term `(2pir dr)` is the area of this elemental ring where `2pir` is the <a href="https://interviewquestions.tuteehub.com/tag/length-1071524" style="font-weight:bold;" target="_blank" title="Click to know more about LENGTH">LENGTH</a> and dr is the thickness. <br/> `:.dm=(2M)/(R^(2))rdr` <br/> `:.dI=(2M)/(R^(2))r^(3)dr` <br/> The moment of inertia (I) of the entire disc is, <br/>`I=intdI` <br/> `I=int_(0)^(R)(2M)/(R^(2))r^(3)dr=(2M)/(R^(2))int_(0)^(R)r^(3)dr` <br/> `K=(2M)/(R^(2))[(r^(4))/4]_(0)^(R)=(2M)/(R^(2))[(R^(4))/4-0]` <br/> `I=1/2MR^(2)`</body></html>


Discussion

No Comment Found

Related InterviewSolutions