InterviewSolution
Saved Bookmarks
| 1. |
Discuss maxima/minima of f(x) = (x)/(1 + x tan x), x in (0, (pi)/(2)) |
|
Answer» SOLUTION :`F'(x) = (1 - x^(2)sec^(2)x)/((1 + x TAN x)^(2))` `= (sec^(2)X (cos x + x)(cos x - x))/((1 + x tan x)^(2))` Now the sign of the derivative DEPENDS on the factor 'cos x - x' only. To check the sign of 'cos x - x', we draw the graphs of y = x and y = cos x. 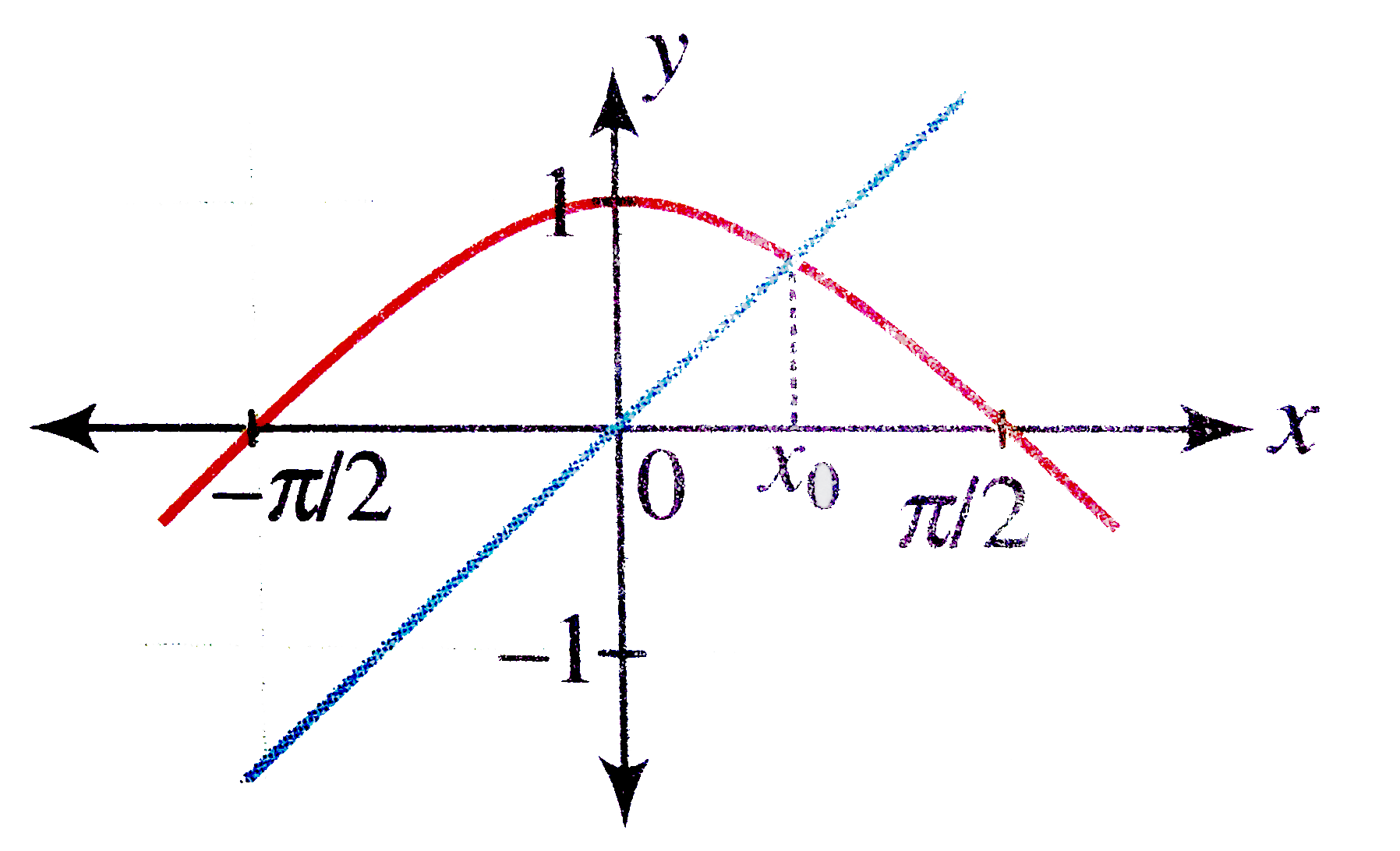 Clearly, `f' (x_(0)) = 0` and `f'(x) gt 0 AA x in (0, x_(0))` `f'(x) lt 0 AA x in (x_(0), pi//2)` Thus, `x = x_(0)` is the only point of maxima for y = f(x). |
|