InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
Draw the graph of f(x) = x^(2)e^(-|x|) i) Find the point of maxima/minima. ii) Find the asymptote is any. iii) Find the range of the function. iv) Find the number of roots of the equation f(x)=1 |
|
Answer» Solution :we have `f(x) = x^(2)e^(-|x|)` Clearly, `f(x)=f(-x)`. So `f(x)` is an even function. Hence the graph is SYMMETRICAL about the y-axis. For `x ge0, f(x) = x^(2)e^(-x)` Now `f^(')(x) = -x^(2)e^(-x) + 2xe^(-x) =XE^(-x)(2-x)` `f^(')(x) = -x^(2)e^(-x)+2xe^(-x) = xe^(-x)(2-x)` `f^(')(x)=0 rArr x=0` or `x=2` `f(0) =0` and `underset(x to infty)"lim"x^(2)/e^(x) = underset(x to infty)"lim"(2x)/e^(x)=underset(x to infty)2/e^(x)=0` So x=2 is the pont of maxima. Hence the graph of `f(x)` is as shown in the following FIGURE. 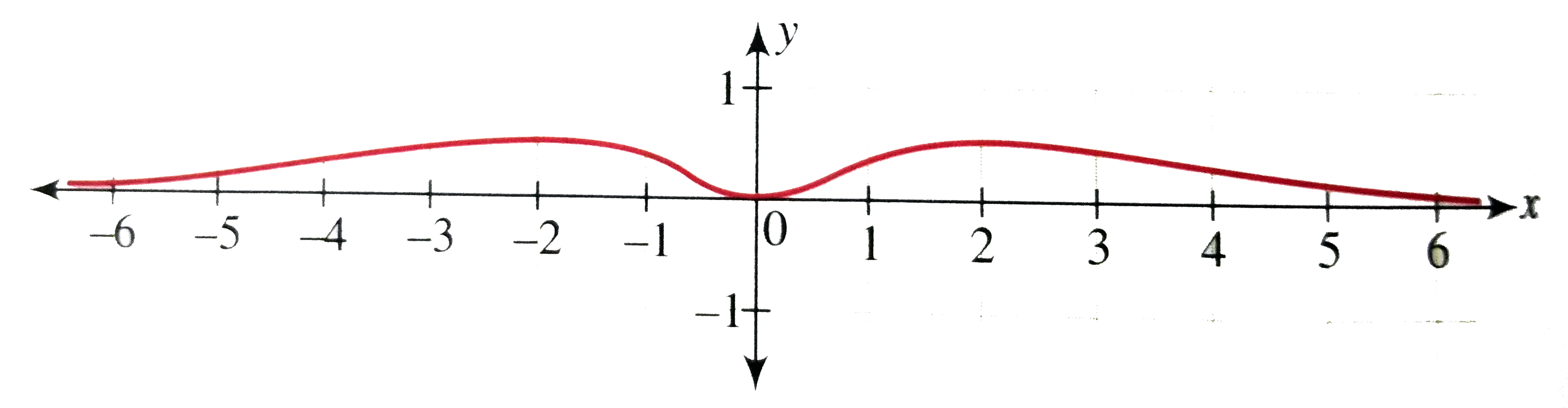 SINCE, `f(x)` is differentiable at `x=0`,the graph touches the x-axis at x=0 The x-axis is also asymptote to the curve. Also since `f(x)` is an even function, `x=-2` is also the point of maxima. RANGE of the function is `[0,f(2)]` or `[0, 4//e^(2)]` Clearly, `f(x) ne 1`, hence `f(x)=1` has no roots. |
|