InterviewSolution
Saved Bookmarks
| 1. |
Draw the graph of the function f(x) = 2x^(2)-log_(e)|x| |
|
Answer» Solution :We have `f(x) = 2x^(2)-log_(e)|x|, x ne 0` Clearly, `f(x)` is an even function, HENCE its graph is SYMMETRICAL about the y-axis. `underset(xto 0^(+))"lim"(2x^(2)-log_(e)|x|)=infty` and `underset(x to +-infty)"lim"(2x^(2)-log_(e)|x|)=infty` (as difference between the value of `2x^(2)` and ln`|x|` is infinite, `log_(e)|x|` increases very slowly, but `2x^(2)` increases faster) ALSO `f^(')(x) = 4x-1/x = (4x^(2)-1)/(x)` `f^(')(x)=0 RARR x = +-1/2` From the limiting values of the function at x=0 and at inifinity, we can conclude that `x=+-1/2` are points of minima. From the above discussion, the graph of the function is as shown in the FOLLOWING figure. 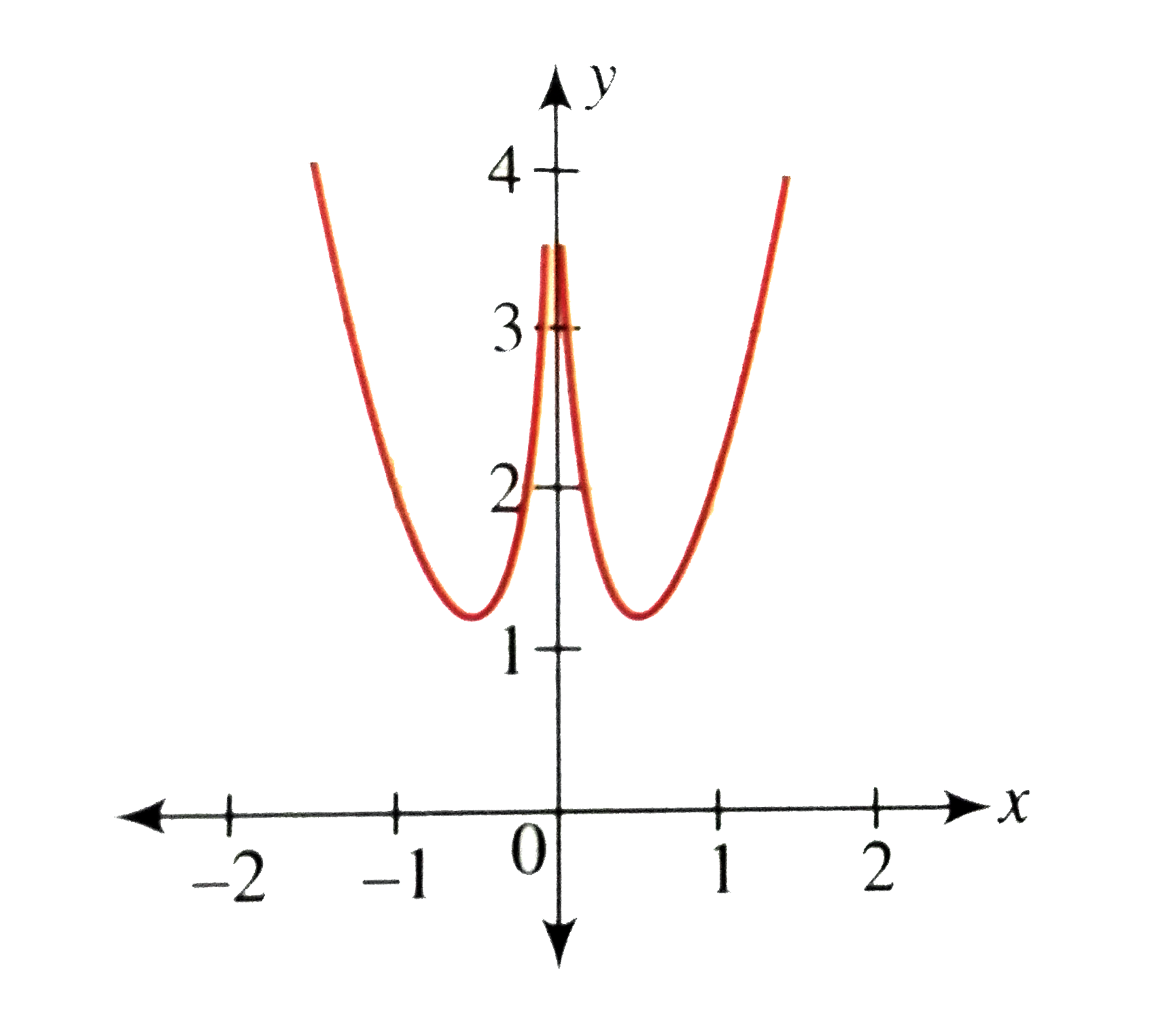
|
|