InterviewSolution
Saved Bookmarks
| 1. |
Draw the graph of the function f(x) = |(x+ (1)/(2))[x]|, -2 le x le 2, where [*] denotes the greatest integer function. Find the points of discontinuity and non-differentiability. |
|
Answer» Solution :Here, `""F(X)= |(x+ (1)/(2))[x]|, -2 le x le 2` `rArr""f(x)= {{:(|(x+(1)/(2))(-2)|",",, -2le xlt -1),(|(x+(1)/(2))(-1)|",",,-1LE xlt 0), (|(x+ (1)/(2))(0)|",",,0 le x lt1),(|(x+ (1)/(2))(1)|",",,1lexlt 2),(|(3)/(2)*2|",",,x=2):}` `rArr""={{:(-(2x+1)",",,-2lexlt-1),(-(x+1//2)",",,-1le x lt -1//2),((x+1//2)",",,-(1)/(2)le x lt 0),(0",",,0LE x lt 1),(x+ (1)/(2)",",,1 le x lt 2),(3",",,x=2):}` The graph of the function is as shown in the following figure. 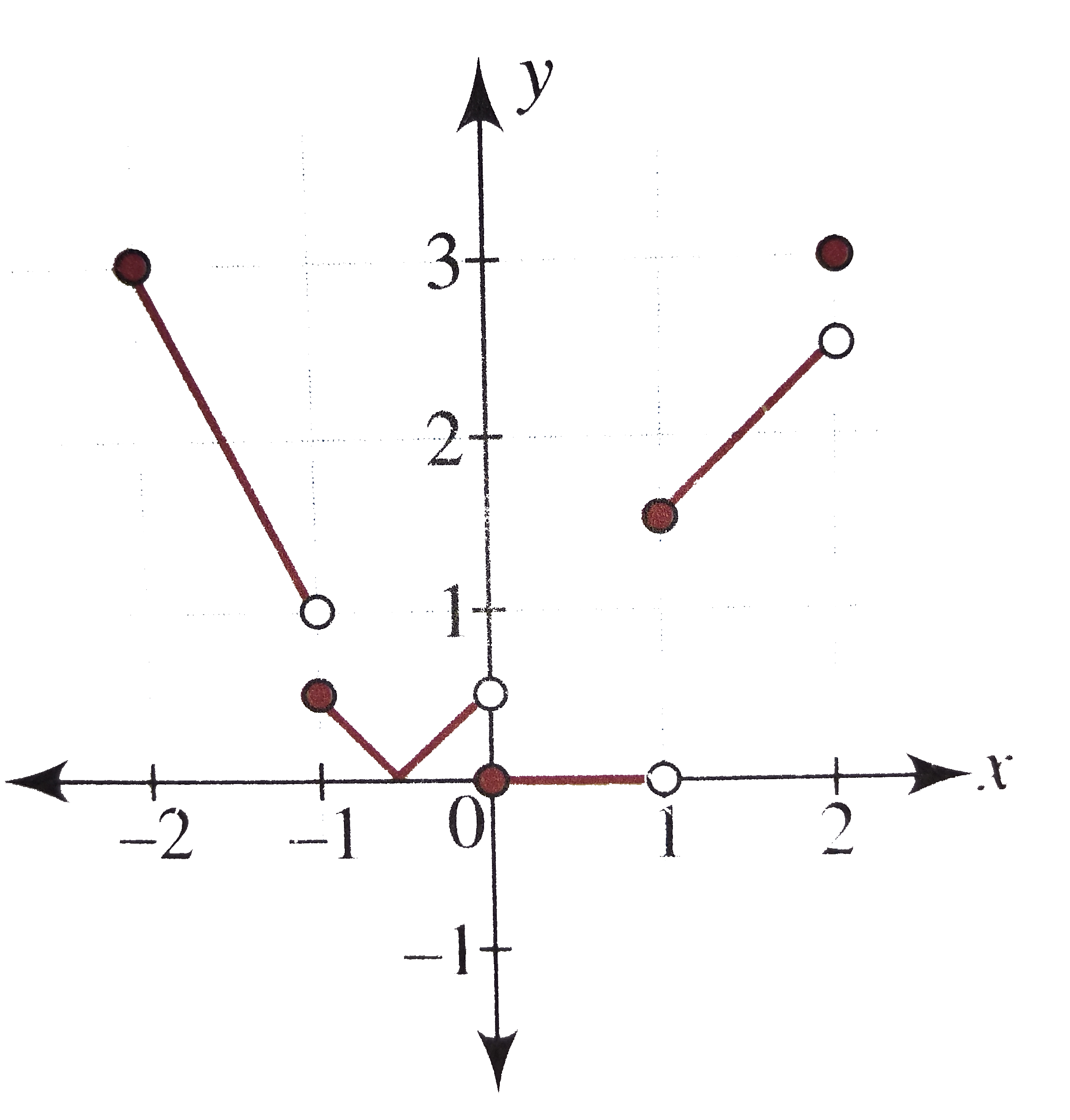 From the figure, `f(x)` is not continuous as `x= { -1, 0, 1, 2}` as at these points, the graph is broken and `f(x)` is not differentiable. At `x= {-1, (-1)/(2), 0, 1, 2}` as at `{-1, 0, 1, 2}`, the graph is broken and `x=-1//2`, there is a sharp edge. |
|