InterviewSolution
Saved Bookmarks
| 1. |
Draw the graph of the relation 4y^(2)=x^(2)(4-x^(2)) |
|
Answer» SOLUTION :We have `4y^(2)=x^(2)(4-x^(2))` `therefore y=+-1/2 sqrt(x^(2)(4-x^(2)))` `therefore y=+-x/2sqrt(4-x^(2))` Let us first draw the graph of `y=f(x) = x/2sqrt(4-x^(2))` Clearly, the domain is `[-2.2]` Now, `f(0)=f(-2)=f(2)=0` Also for `x lt0, f(x)lt0` and for `x GT0, f(x) gt0` Now `(dy)/(DX) = 1/2sqrt(4-x^(2))-x/2x/sqrt(4-x^(2))` `RARR 4-x^(2)=x^(2)` `rArr x=+-sqrt(2)` Since `f(x) gt 0` for `x lt 0` and `f(0)=f(2)=0, x=sqrt(2)` is the point of maxima and `x=-sqrt(2)` is the point of minima. `f(sqrt(2))=1, f(-sqrt(2))=-1` Also `f(x)` is an odd function. Hence, the graph of the function is as shown in the following figure. 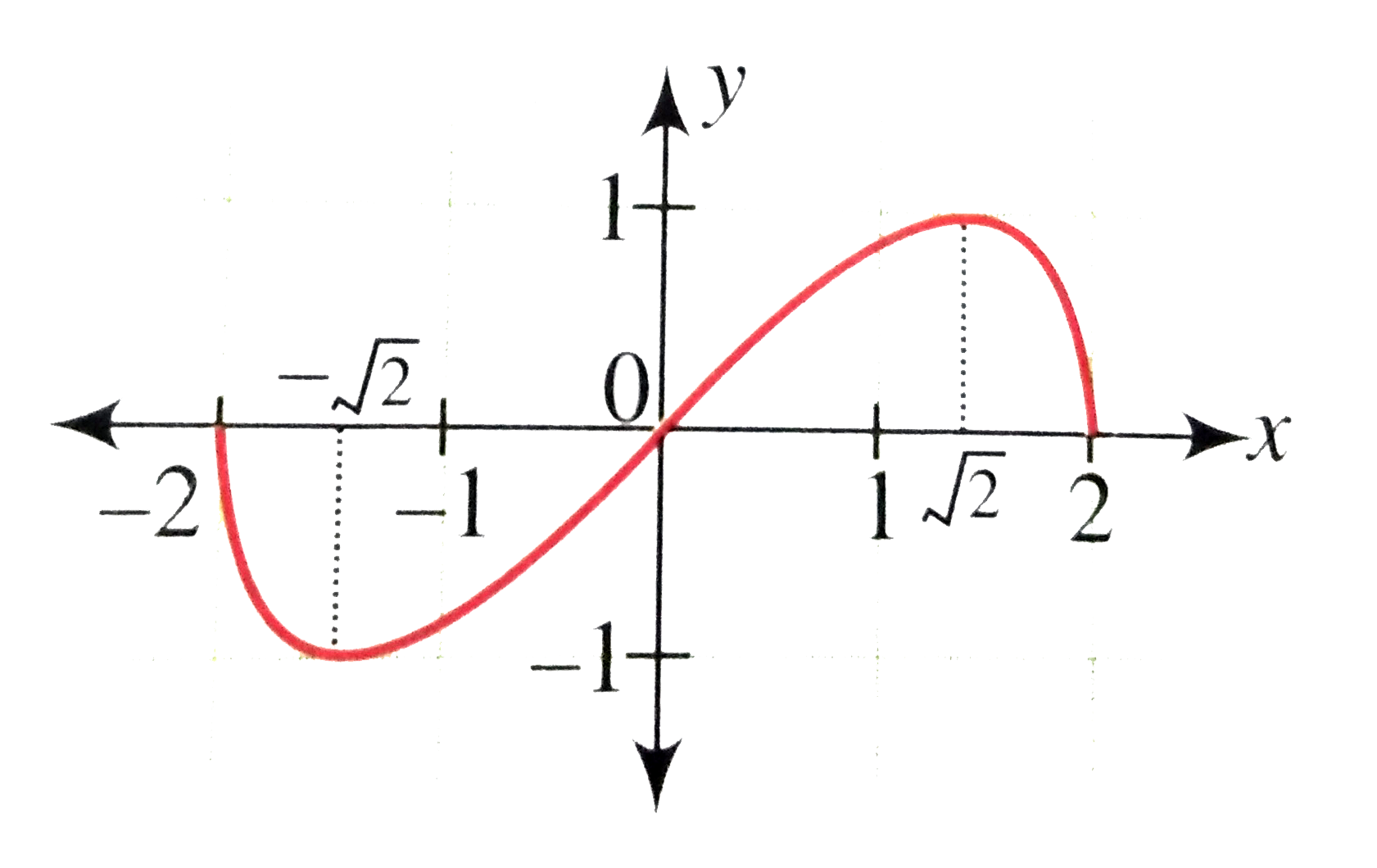 Graph of `y=-x/1sqrt(4-x^(2))` can be obtained by reflecting the above graph in the x-axis. Hence, the graph of the relation `4y^(2)=x^(2)(4-x^(2))` is a FOLLOWS. 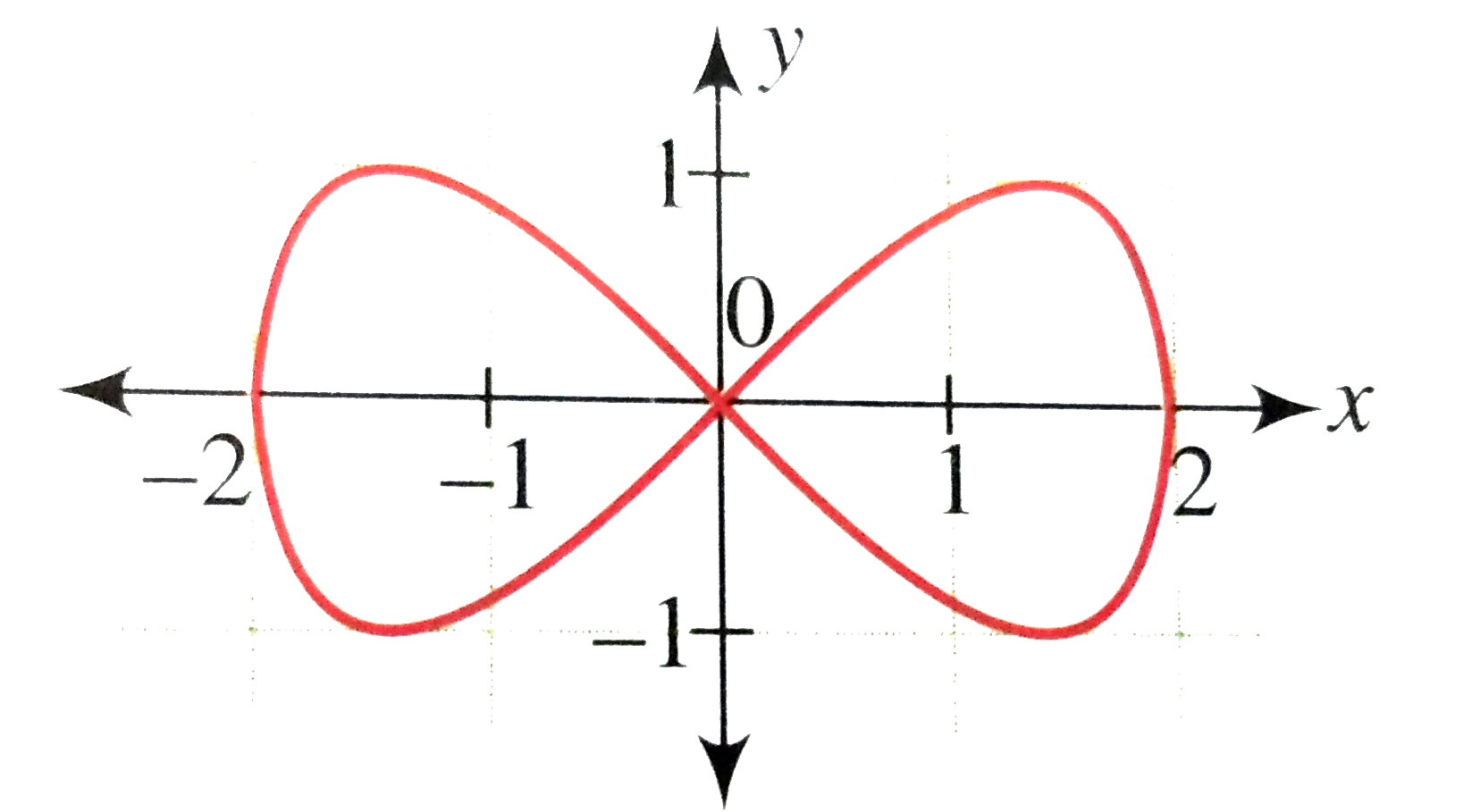
|
|