InterviewSolution
Saved Bookmarks
| 1. |
Draw the graph of the relation y^(2)=x^(2)(1-x) |
|
Answer» Solution :We have `y^(2)=x^(2)(1-x)` `rArr y=+-xsqrt(1-x)` Let us first draw the graph of `y=f(x) = xsqrt(1-x)`. This FUNCTION is defined if `x le1` For `0 ltx le1, y gt0` andfor `x lt 0, y lt 0` Also `y=0 rArr x =0,1` When `x to -INFTY, y to -infty` `f^(')(x) = (1.sqrt(1-x)-x/(2sqrt(1-x)))` `(2-3x)/(2sqrt(1-x))` `f^(')(x)=0 therefore x=2/3`, which is the point of maxima. Thus, graph of the function is as shown in the ADJACENT figure. 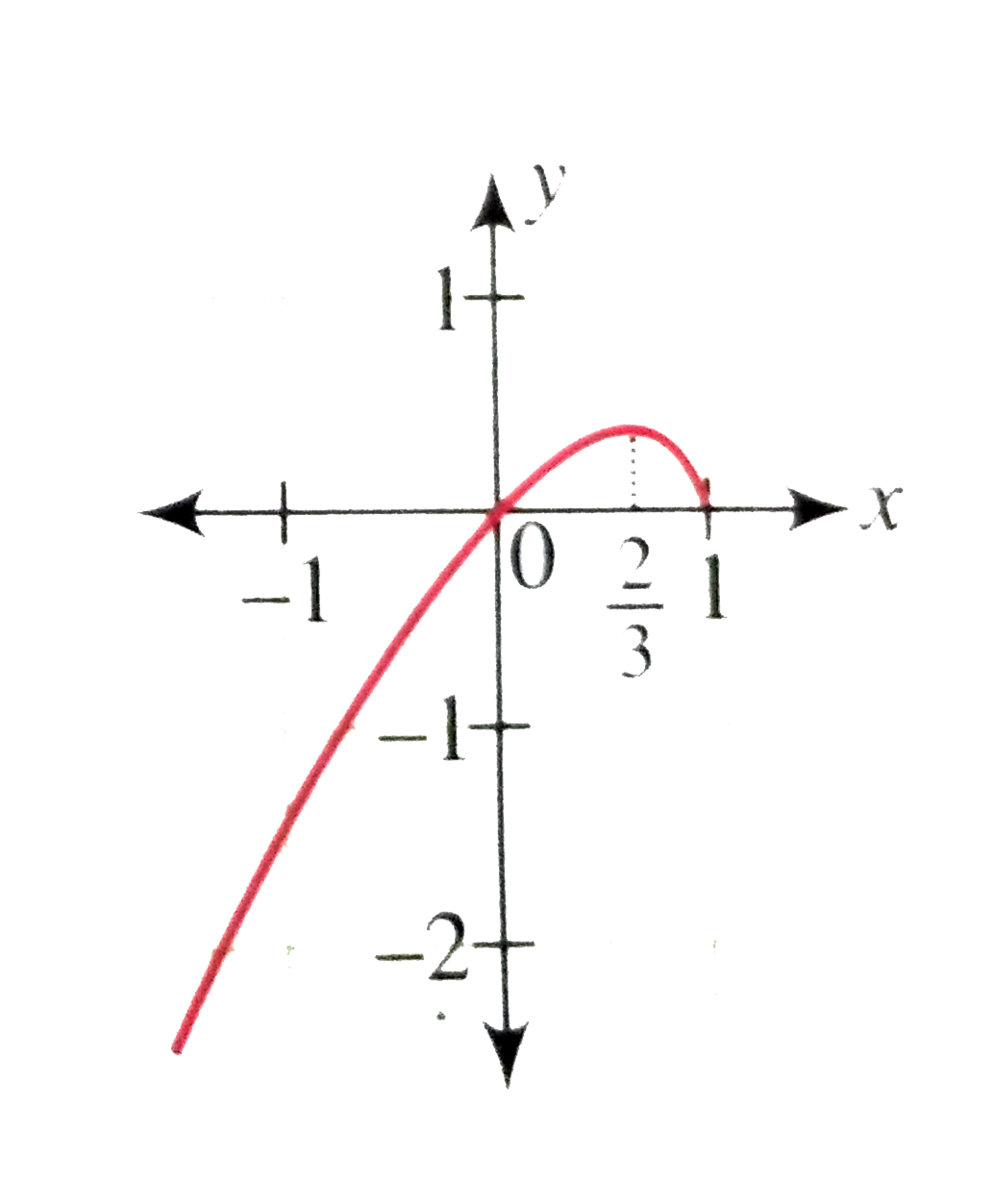 To draw the graph of `y=-xsqrt(1-x)`, reflect the graph above the graph in the x-axis. HENCE the graph of the relation `y^(2)=x^(2)(1-x)` is as shown in the following figure. 
|
|