InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
Draw the graph of y=(1-x^(2))/(1+x^(2)) and hence draw the graph of y=cos^(-1).(1-x^(2))/(1+x^(2)). |
|
Answer» Solution :We have `y=f(x)=(1-x^(2))/(1+x^(2))=(2)/(1+x^(2))-1` Clearly, the domain is R. `y=f(x)` is an even funtion, so the graph is SYMMETRICAL about the y-axis. Let us first draw the graph of r`x in [0,oo)`. `f(0)=1` `f(x)=0 :. x=1` `underset(xrarroo)lim((2)/(1+x^(2))-1)=-1` THUS, from `f(0)=1,((2)/(1+x^(2))-1)` decreases intersecting the x-axis at (1,0) and APPROACHES '-1' as x approaches `'oo'`. Also `f'(x)=(-4X)/((1+x^(2))^(2))`, so f(x) is differentiable at x = 0. Hence the graph of `y=f(x)` is as shown in the FOLLOWING figure. 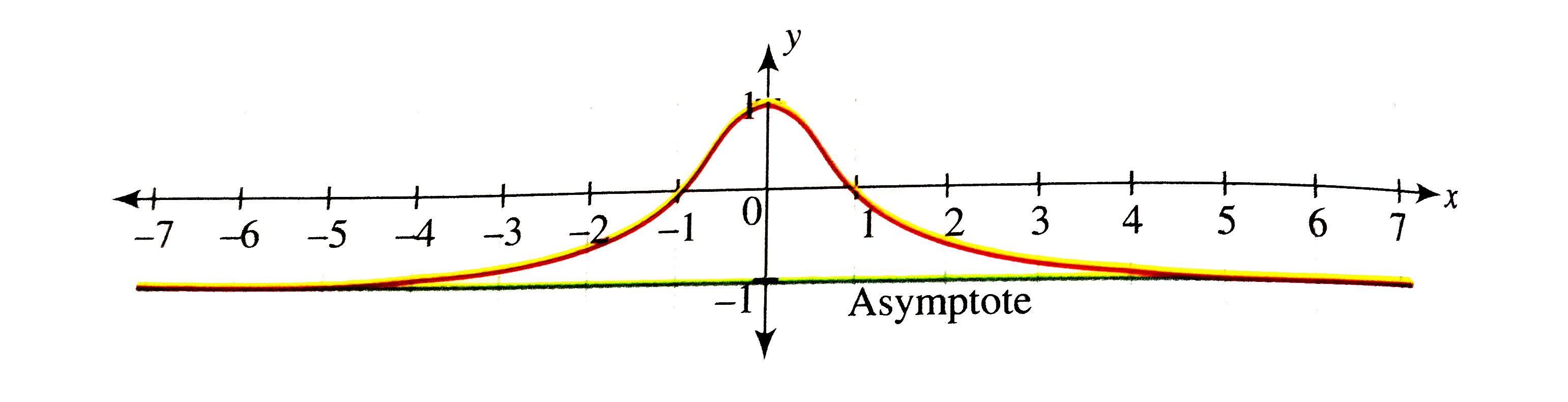 Since the range of `(1-x^(2))/(1+x^(2))` is (-1,1), the domain of `g(x)=cos^(-1)f(x)=cos^(-1).(1-x^(2))/(1+x^(2))` is also R `g(0)=cos^(-1)(1)=0` and `underset(xrarroo)limcos^(-1)((1-x^(2))/(1+x^(2)))=underset(xrarroo)lim cos^(-1)((2)/(1+x^(2))-1)=pi` Thus, the value of g(x) increases from '0' and approaches `'pi'` as x approaches `'oo'`. Also g(x) is an enven function, so the graph is symmetrical about the y-axis. Also `g'(x)=(f'(x))/(sqrt(1-(f(x))^(2)))` g'(0) does not exist as f(0)=1, so g(x) is non-differentiable at x=0. Hence the graph of `y=g(x)` can be drawn as shown in the following figure.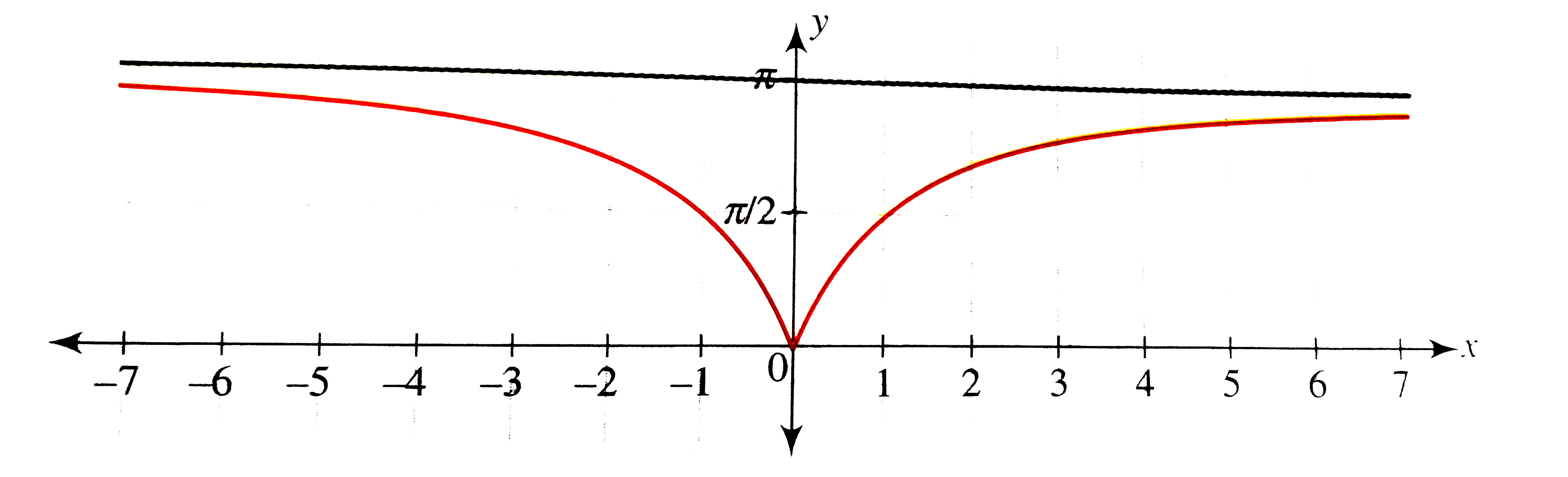 
|
|