InterviewSolution
Saved Bookmarks
| 1. |
Draw the graph of y=e^(x)+e^(-2x) |
|
Answer» Solution :We have `y=f(x)=e^(x)+e^(-2x)` Clearly, the doamin of the function is R. `f(0) =1+1=2` ALSO `f(x) gt 0, AA x in R` `f^(')(x) = e^(x)-2e^(-x)= e^(-2x)e^(3x-2)` `f^(')(x)=0 therefore e^(3x)=2` or `x=1/3log2` `f(1/3log2) e^(1/3log2) + e^(-2/3)log2=2^(1//3) + 2^(-2//3) = 3/2^(2/3)` `f(x)` DECREASES in `(-INFTY, 1/3 log2)` and increases in `(1/3log2, infty)` Hence the graph of the function is as shown in the following figure. 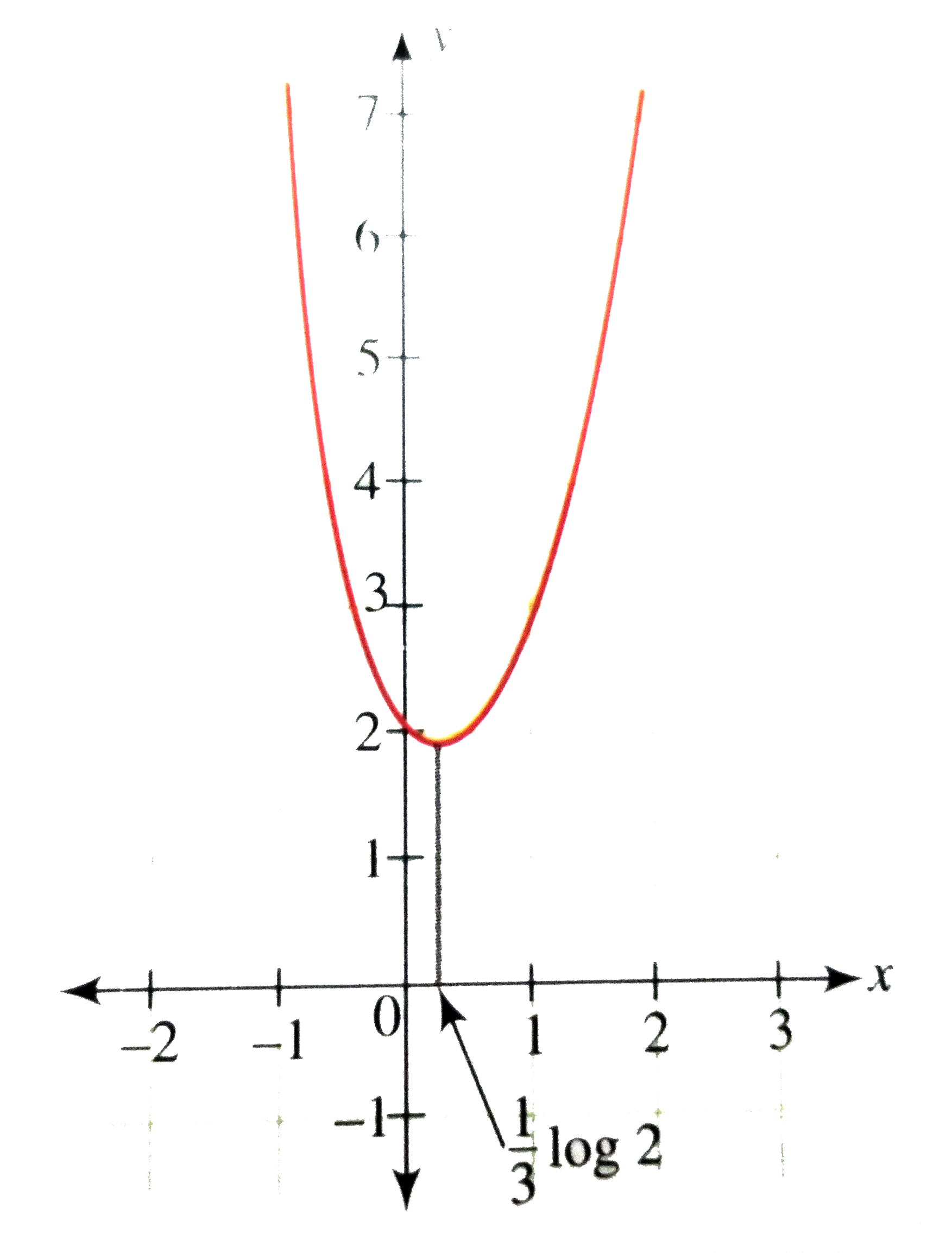
|
|