InterviewSolution
Saved Bookmarks
| 1. |
Draw the graph of y= [x]+ sqrt(x-[x]), where[*] denotes the greatest ineger function. |
|
Answer» Solution :`y= f(X) = [x] + sqrt(x-[x])` For `0 le x LT 1, y = sqrtx`,the graph of which is PART of parabola `y^(2)=x` lying above the x-axis. For `1 le x lt 2, y=1 + sqrt(x-1)`, the graph of which is part of the parabola `(y-1)^(2)=x-1` lying above the axis of the parabola `y=1`. THUS, all the branches of `y=f (x) ` are part of different parabolas. Also we can see that in each interval `y= f(x)` is an increasing function. Hence the graph of`y= f(x)` is as SHOWN in the following figure. 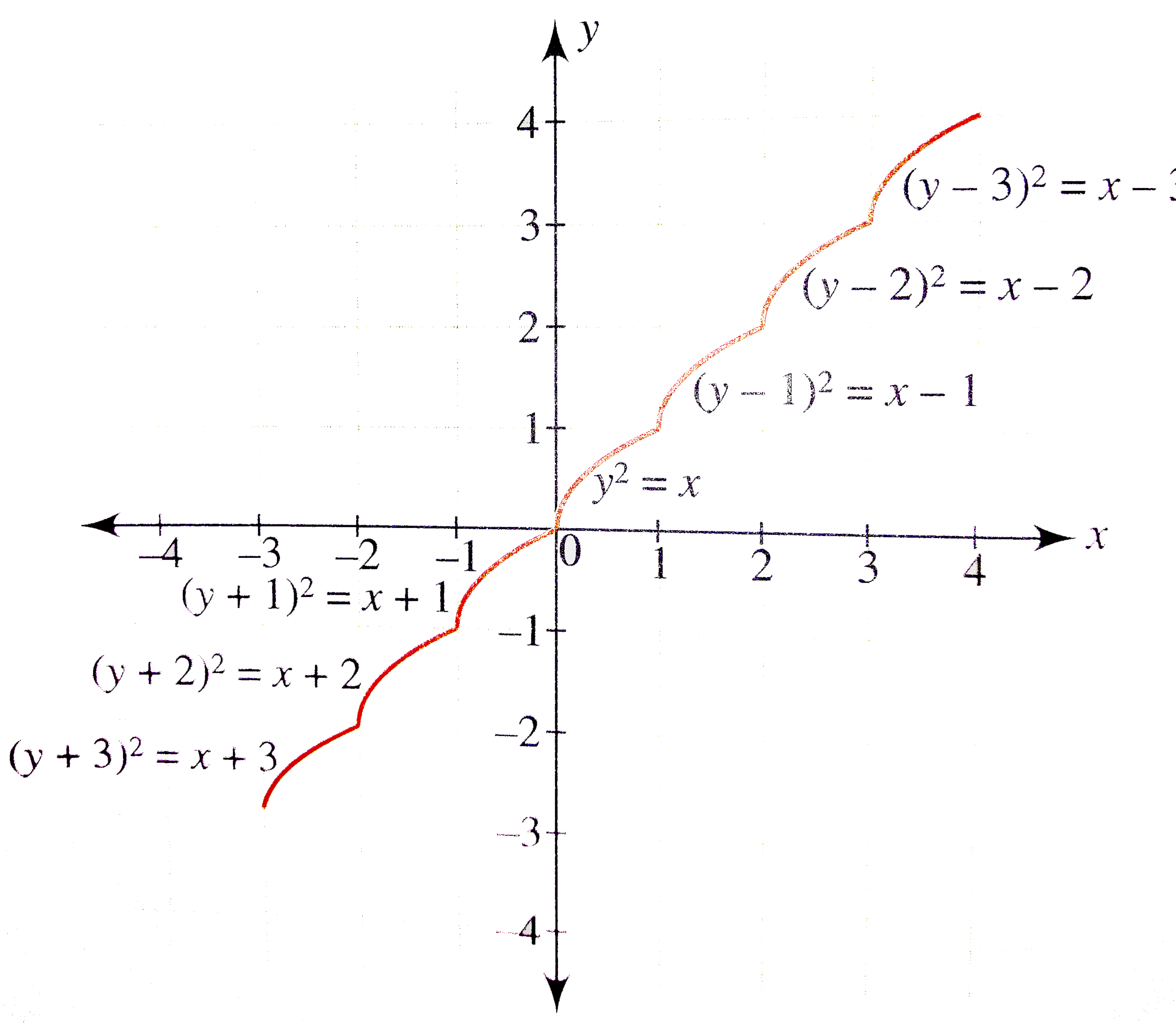
|
|