InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
Find the area of the region {(x,y): x^2 +y^2 le 2ax , y^2 le ax , x le 0 , y le 0 } |
|
Answer» Solution :Clearly we have to find the area of the region lying in the first quadrant `(x ge 0, y ge 0 )` included between the CIRCLE `x^(2)+y^(2)=2ax` and the PARABOLA `y^2 =ax` Thus , the equations of the given curves are `x^2+y^2 =2ax…(i)` and`y^2 =ax` ...(II) Now , clearly `x^2+y^2=2ax ` is a circle with its CENTER `B(a,0)` and radius `=a` units And `y^2=ax ` is parabola with `O(0,0)` as its vertexand the x-axis as its axis. We can draw its figure as shown . Their points of intersection may be obtained by solving `(i)` and `(ii)` and keeping in view that `x ge 0 and y gt 0` Using `(ii)` in `(i)` ,we get `x^2-ax =0 rArr x(x -a) =0` `rArr x=0 or x =a` Now `(x=0 rArr y=0 )` and `(x=a rArr y=a)` Thus, two curves intesect at O(0,0) and A(a,a) `therefore" required area " =UNDERSET(0)overset(a)int sqrt(2ax -x^2)dx - underset(0)overset(a)int sqrt(ax)dx` `=underset(0)overset(a)intsqrt(a^2-(x-a)^2)dx -sqrt(a).underset(0)overset(a)int sqrt(x)dx ` `=[((x-a)sqrt(a^2-(x-a)^2))/(2)+a^2/2 sin^(-1)""((x-a)/a)]_0^a-sqrt(a)[2/3x^(3//2)]_0^a` `={a^2/2sin^(-1)(0)-a^2/2 sin^(-1)(-1)-2/3a^2}` `=((pia^2)/4-2/3a^2)`sq units Hence, the required area is `=((pia^2)/4-2/3a^2)` sq units .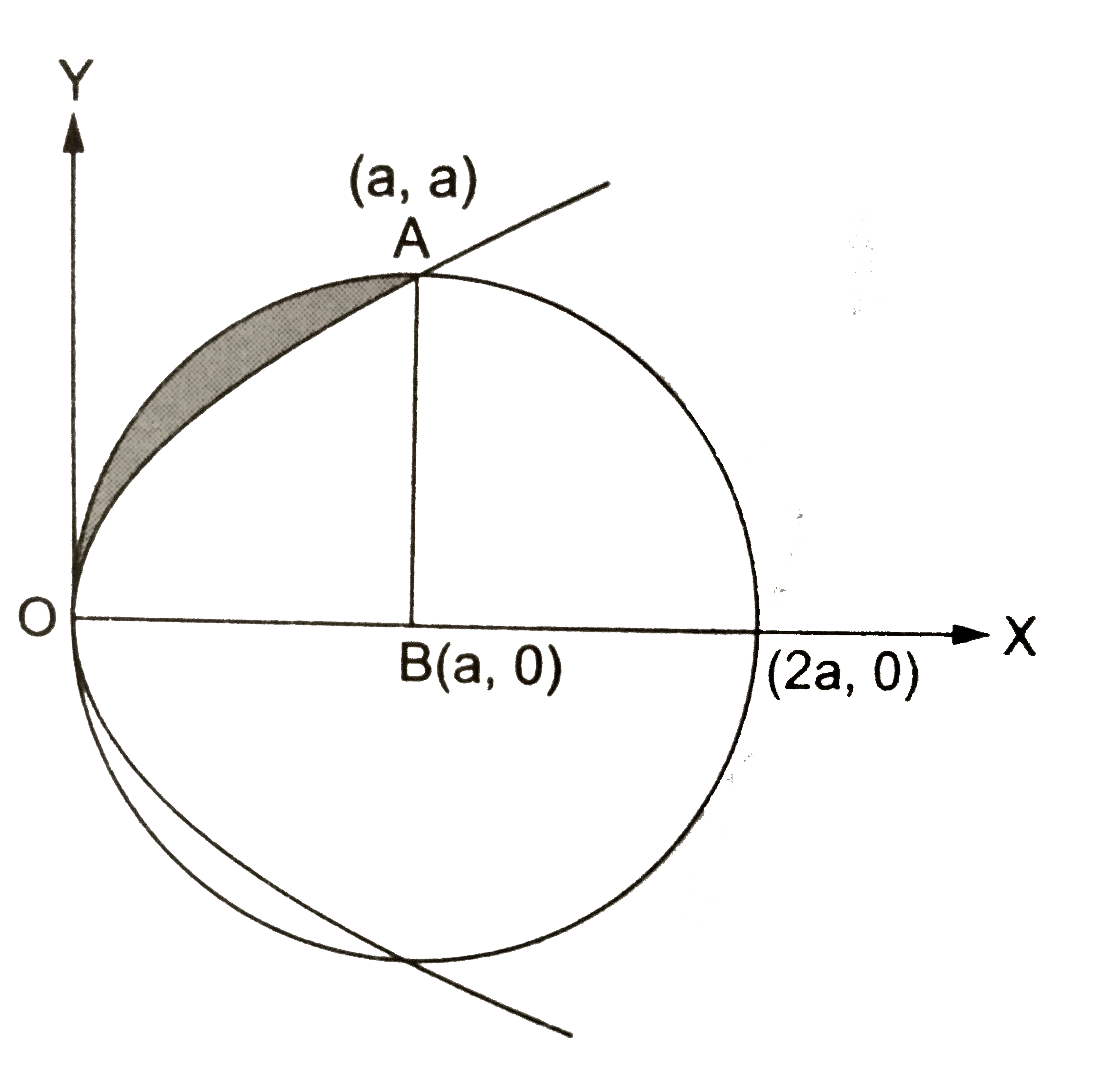 
|
|