InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
Find the ratio of the areas of two regions of the curve C_(1) -= 4x^(2) + pi^(2)y^(2) = 4pi^(2) divided by the curve C_(2) -= y = -(sgn(x - (pi)/(2)))cos x (where sgn (x) = signum (x)). |
|
Answer» Solution :`4x^(2) + pi^(2)y^(2) = 4pi^(2)` `therefore` `C_(1) : (x^(2))/(pi^(2)) + (y^(2))/(4) = 1`, which is an ellipise. Curve `C_(2) : y = -sgn (x - (pi)/(2)) cos x` `=({:(-cos x",", x gt (pi)/(2)),(cos x",", x LT (pi)/(2)),(0",", x = (pi)/(2)):}` Graphs of `C_(1)` and `C_(2)` are as shown in the following figure. 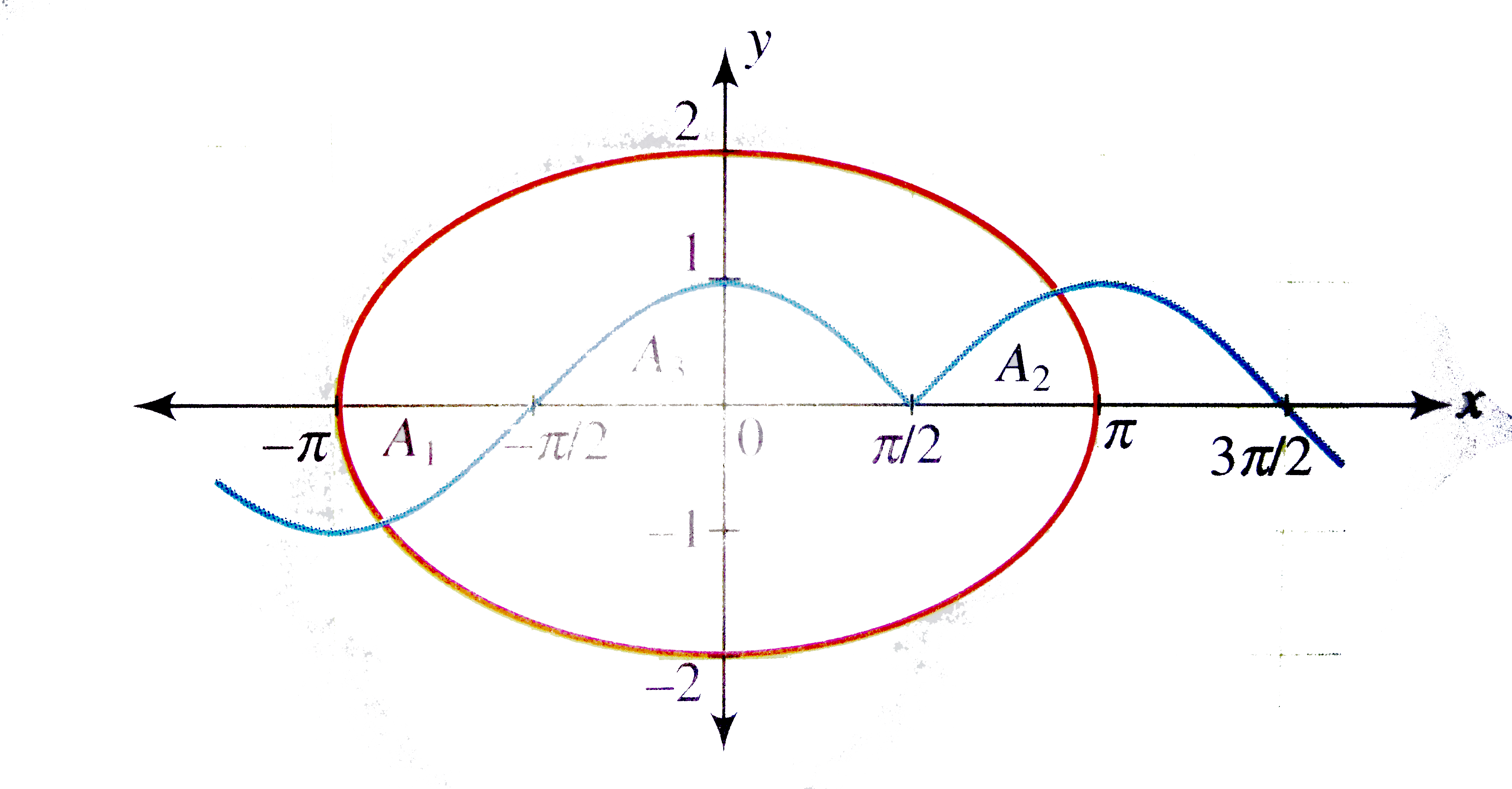 From the symmetry of the curves, the areas of regions `A_(1)` and `A_(2)` are EQUAL. Area of ellipse is `pi(pi)(2) = 2pi^(2)`. Area of ellipse above the x - axis is `pi^(2)`. Now the area bounded by y = cos x and the x - axis `(A_(3))` is 2 SQ. units. So the area OFTHE portion of the ellipse above the curve `C_(2)` is `pi^(2) - 2` (as the areas of regions `A_(1)` and `A_(2)` are same) So the area of the portion of the ellipse below the curve `C_(2)` is `pi^(2) + 2`. Hence the required ratio is `(pi^(2) - 2)/(pi^(2) + 2)` |
|