InterviewSolution
Saved Bookmarks
| 1. |
If a circle of radius R passes through the origin O and intersects the coordinate axes at A and B, then the locus of the foot of perpendicular from O on AB is |
|
Answer» `(x^(2)+y^(2))^(2)=4R^(2)x^(2)y^(2)` 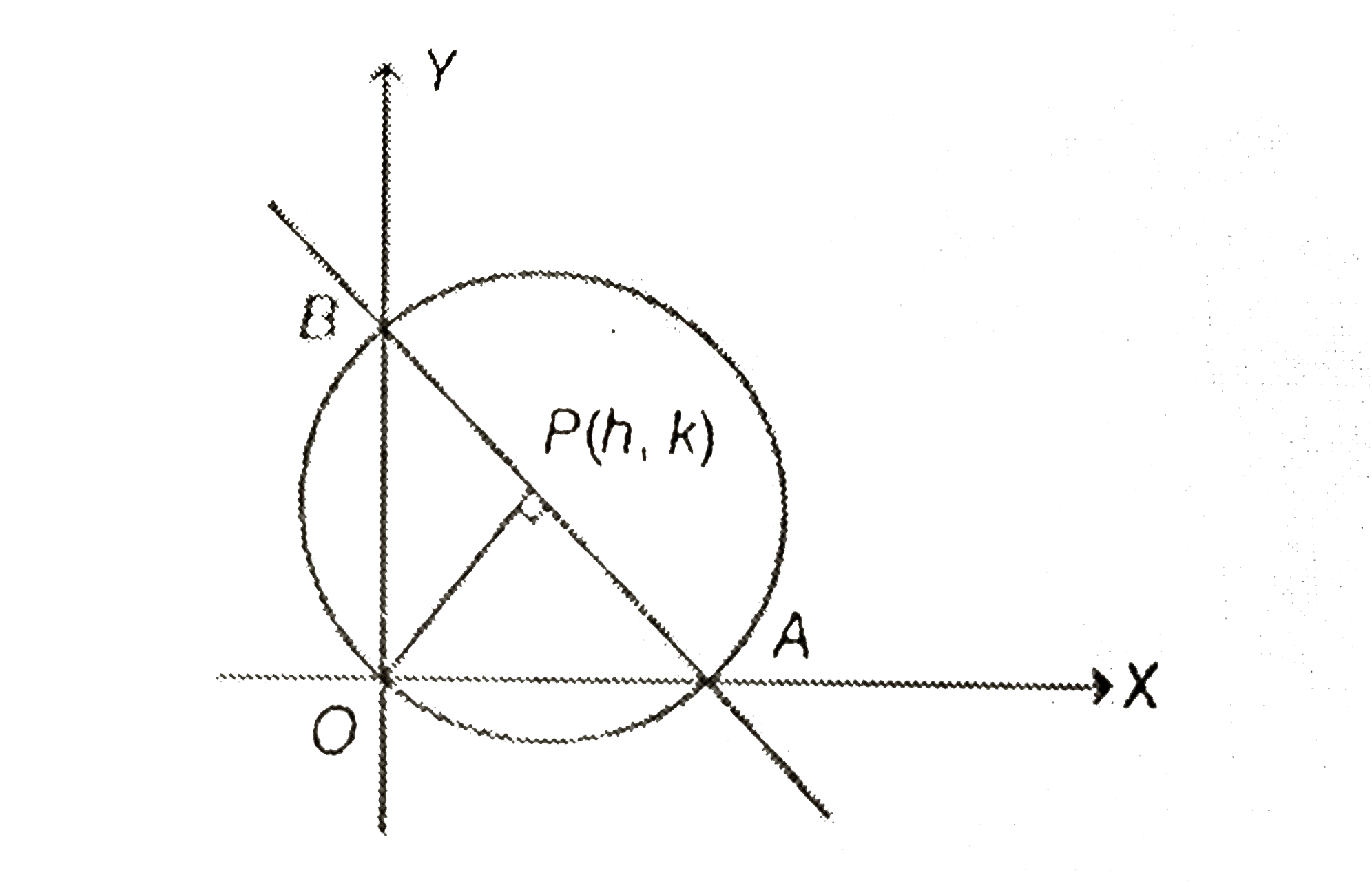 `therefore` Line AB is perpendicular to line OP, so slope of line `AB = -(h)/(k)`[`therefore` product of slope of two perpendicular line s is (-1)] Now, the equation of line AB is `y-k=-(h)/(k)(x-h)rArrhx+ky=h^(2)+k^(2)` or`(x)/(((h^(2)+k^(2))/(h)))+(y)/(((h^(2)+k^(2))/(k)))=1` So, point `A((h^(2)+k^(2))/(h),0) and B(0,(h^(2)+k^(2))/(h))` `therefore Delta AOB` is a RIGHT angled triangle, so AB is ONE of the diameter of the circle having radius R (given). `rArr AB = 2R` `rArrsqrt(((h^(2)+k^(2))/(k))^(2)+((h^(2)+k^(2))/(k)))=2R` `rArr (h^(2)+k^(2))^(2)((1)/(h^(2))+(1)/(k^(2)))=4R^(2)` `rArr(h^(2)+k^(2)) =4R^(2) h^(2)k^(2)` On replacing h by x and k by y, we get `(x^(2)+y^(2))^(3)=4R^(2)x^(2)y^(2)`, which is teh REQUIRED locus. |
|