InterviewSolution
Saved Bookmarks
| 1. |
If nsinx=log_(e)x has exactly 1 root, then find the possible value of n(ninN). |
|
Answer» Solution :`nsinx=log_(e)x` `impliessinx=(log_(e)x)/(n)` For exactly one root, the graph of `y=sinx` must intersect the graph of `y=(log_(e)x)/(n)` exactly once. Maximum value of sin x is 1. 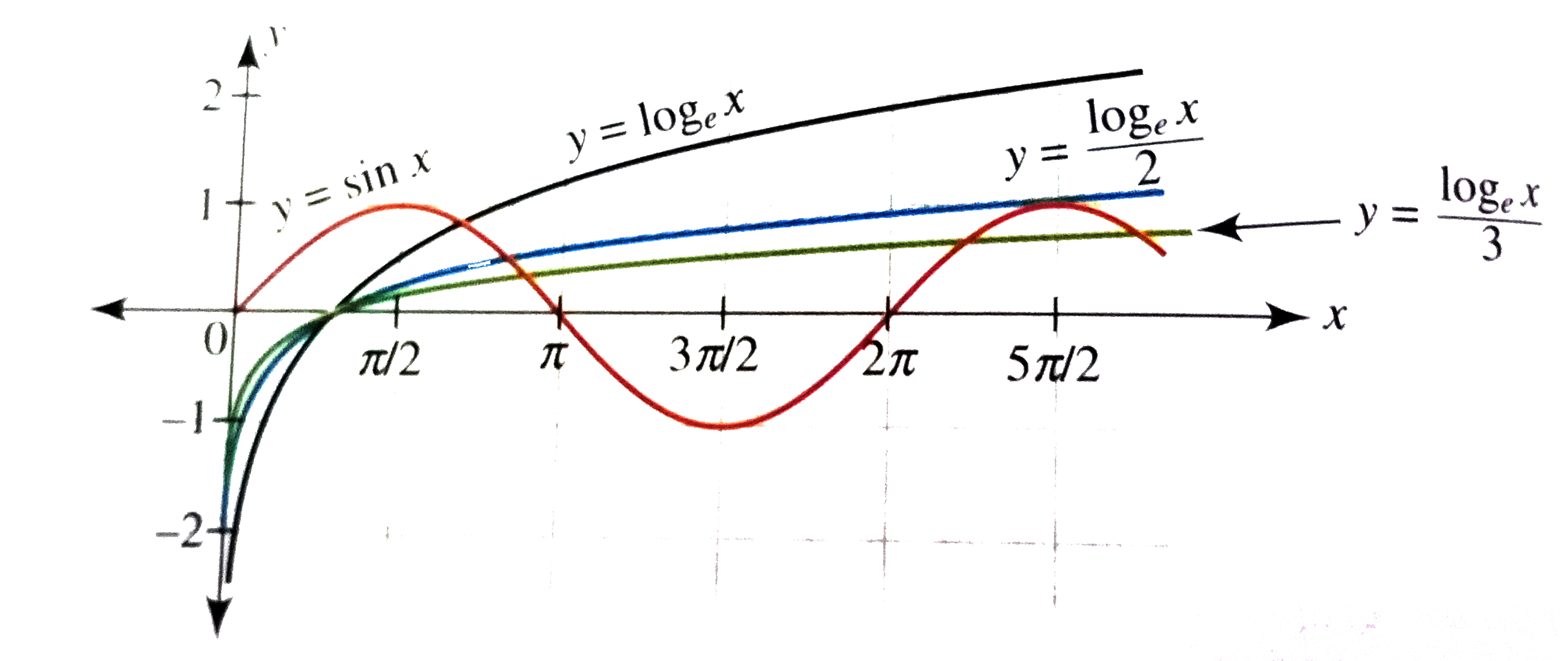 For `n=1,sinx=log_(e)x` Graphs of `y=sinxandy=log_(e)x` intersect only once as shown in the FOLLOWING figure. For `x=e,log_(e)e=1`, hence after `x=e,y=log_(e)x` never meets `y=sinx`. For `n=2,"let"(log_(e)x)/(2)=1:.log_(e)x=2orx=e^(2)lt5pi//2` Hence the graph of `y=(log_(e)x)/(2)` meets `y=sinx` only once. But for `n=3and(log_(e)x)/(3)=1,x=e^(2)gt5pi//2` hence the graph of `y=(log_(e)x)/(3)` MEET the graph of `y=sinx` more than once. So for exactlly one root of the EQUATION `sinx=(log_(e)x)/(n),n=1or2`. |
|