InterviewSolution
Saved Bookmarks
| 1. |
If x in[(4n+1)(pi)/(2),(4n+3)(pi)/(2)] and n in N, then the value of int_(0)^(x)[cos t] dt, is |
|
Answer» `(2n-1)(PI)/(2)-X` Now, `overset(x)UNDERSET(0)int [cos t]dt=overset((4n+1)pi//2)underset(0)int [cos t]dt+overset(x)underset((4n+1)pi//2)int[cos t]dt` `rArr overset(x)underset(0)int [cos t]dt=overset(2npi+pi//2)underset(0)int [cos t]x" dt"+overset(x)underset(2npi+pi//2)int [cos t]dt` 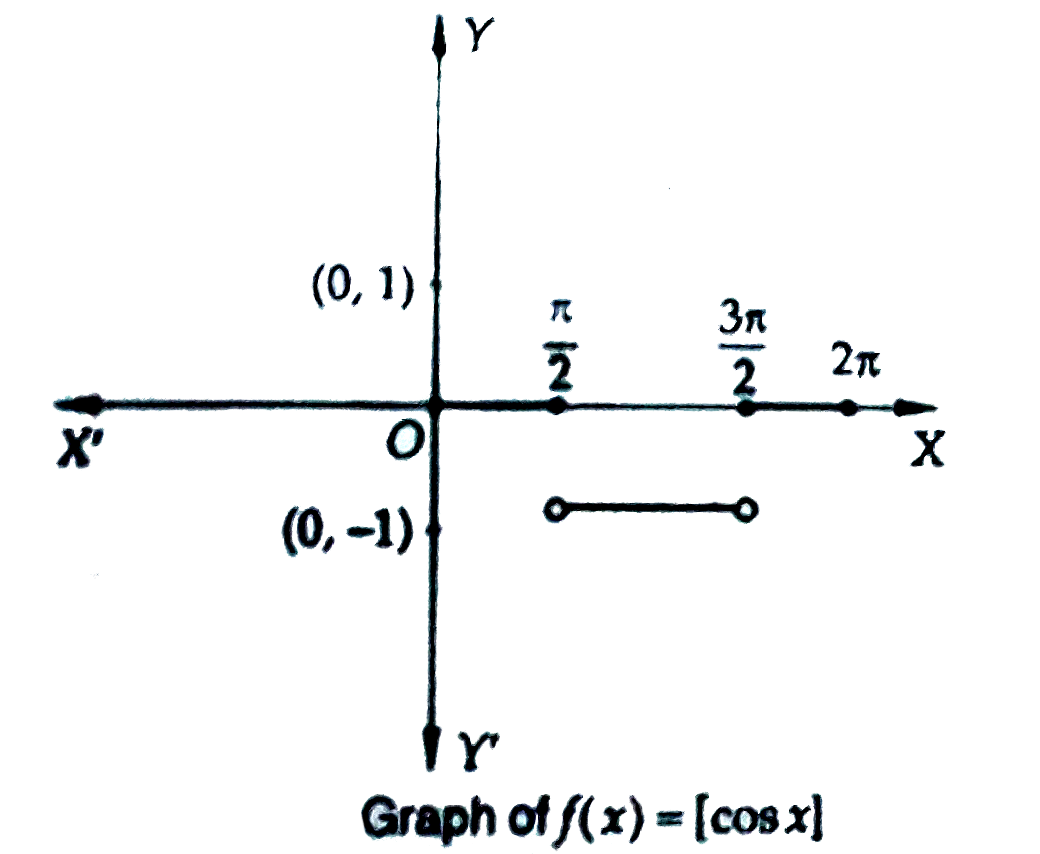 `rArr overset(x)underset(0)int [cos t]dt=overset(2npi)underset(0)int [cos t]dt+overset(2npi+pi//2)underset(2npi)int [cos t]dt+overset(x)underset(2npi+pi//2)int [cos t]dt` `rArr overset(x)underset(0)int [cos t]dt=n overset(2npi)underset(0)int[cos t]dt+overset(pi//2)underset(0)int [cos t]dt+overset(x)underset(2npi+pi//2)int[cos t]dt` `rArr overset(x)underset(0)int [cos t]dt=n[overset(pi//2)underset(0)int 0 dt+overset(3PI//2)underset(pi//2)int (-1)dt+overset(2pi)underset(3pi//2)int 0 dt]+overset(pi//2)underset(0)int 0 dt+overset(x)underset(2npi+pi//2)int -1 dt` `rArr overset(x)underset(0)int [cos t]dt=n[-((3pi)/(2)-(pi)/(2))]-[x-(2n+(pi)/(2))]` `rArroverset(x)underset(0)int [cos t]dt=npi+(pi)/(2)-x=(2n+1)(pi)/(2)-x` |
|