InterviewSolution
Saved Bookmarks
| 1. |
If z_(1), z_(2), z_(3), z_(4) are complex numbers in an Argand plane satisfying z_(1)+z_(3)=z_(2)+z_(4). A compex number 'z' lies on the line joining z_(1) and z_(4) such that Arg((z-z_(2))/(z_(1)-z_(2)))=Arg((z_(3)-z_(2))/(z-z_(2))). It is given that |z-z_(4)|=5,|z-z_(2)|=|z-z_(3)|=6 then |
|
Answer» AREA of triangle formed by `Z,z_(1),z_(2)` is `3sqrt(7)` SQ units and `b/6=6/a` `implies ab=36` `b^(2)+5b-36=0` `implies b=4` 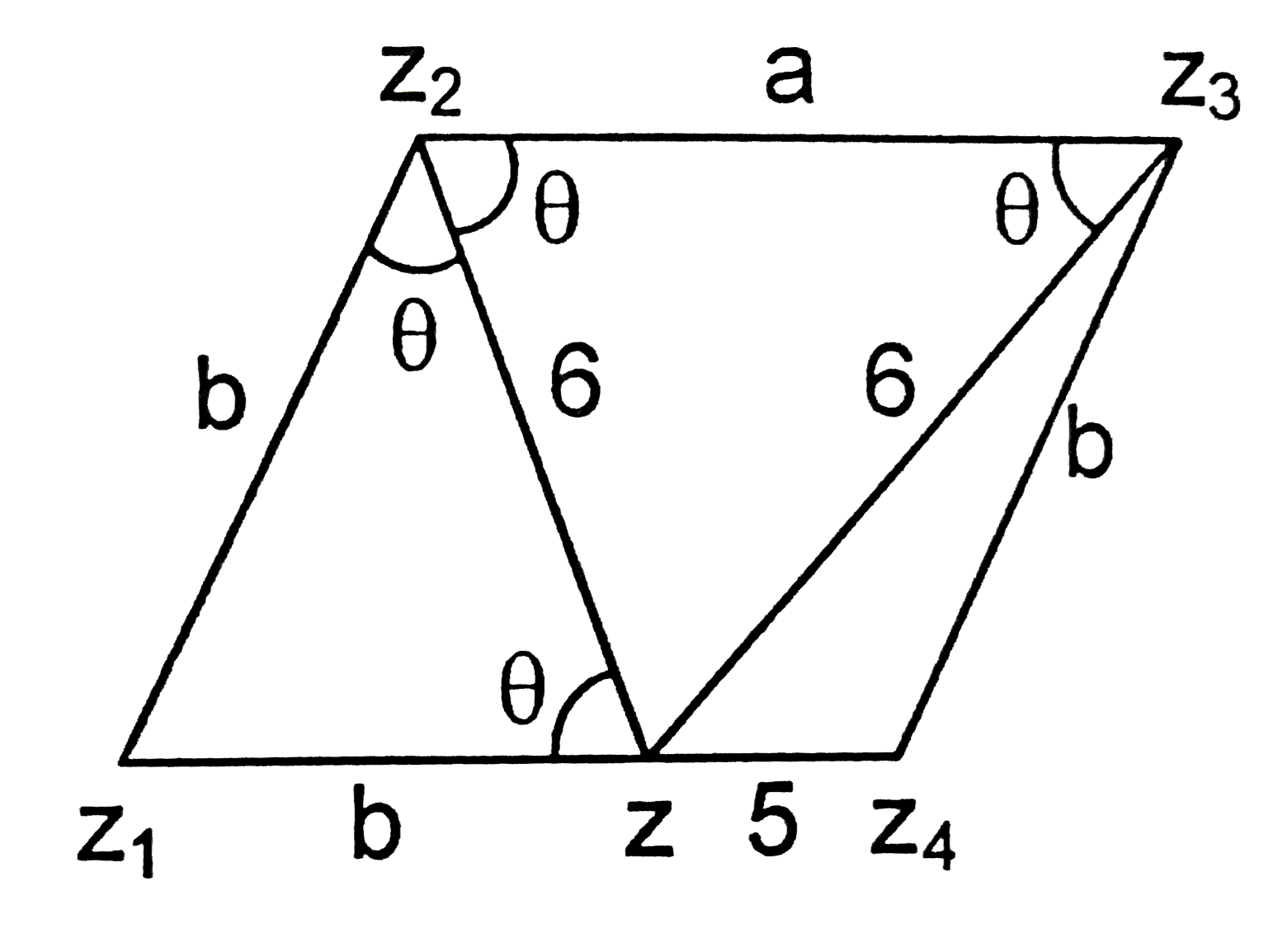
|
|