InterviewSolution
Saved Bookmarks
| 1. |
If Z in C and area enclosed by the curves |Z + bar(Z)| + |Z - bar(Z)| ge 4 and |Z| le 2 is equal to (a pi - b) where a, b in N then the value of is |
|
Answer» Let `Z = x + iy` 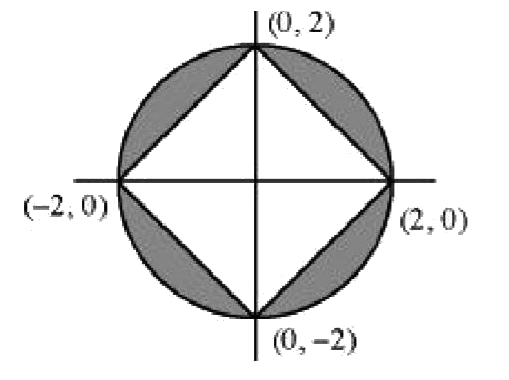 `|x|+|y| ge 2` `|z| le 2` represent INTERIOR part of CIRCLE WHOSE radius is 2 and centre at origin Required area = `pi (2)^(2) - 4.1/2.2 = 4pi - 8` `a = 4, b = 8` then `b/(4a) = 8/16 = 0.5`. |
|