InterviewSolution
Saved Bookmarks
| 1. |
Let A,B, and C be three sets such that A={(x,y)|(x)/(cos theta)=(y)/(sintheta)=5,"where" 'theta'"is parameter"} B= {(x,y)|(x-3)/(cos phi)=(y-4)/(sin phi)=r} C= { (x,y)|(x-3)^(2)+(y-4)^(2)leR^(2)} If phi is fixed and r varies and (A cap B) =1, then sec phi is equal to |
|
Answer» `(5)/(4)` A is set of points which lie of the circle `C_(1) : x^(2)+y^(2) =25` `B = { (x,y)|(x-3)/(cos phi)=(y-4)/(sin phi) =r}` If` phi` varies and r is fixed, then B is the set of all points which lie on a circle `C_(2) : (x-3)^(2) +(y-4)^(2) =r^(2)` And if `phi` is fixed and r varies, then B is the set of all points which lie on the straight line `L : y-4= tan theta ( x-3)`. 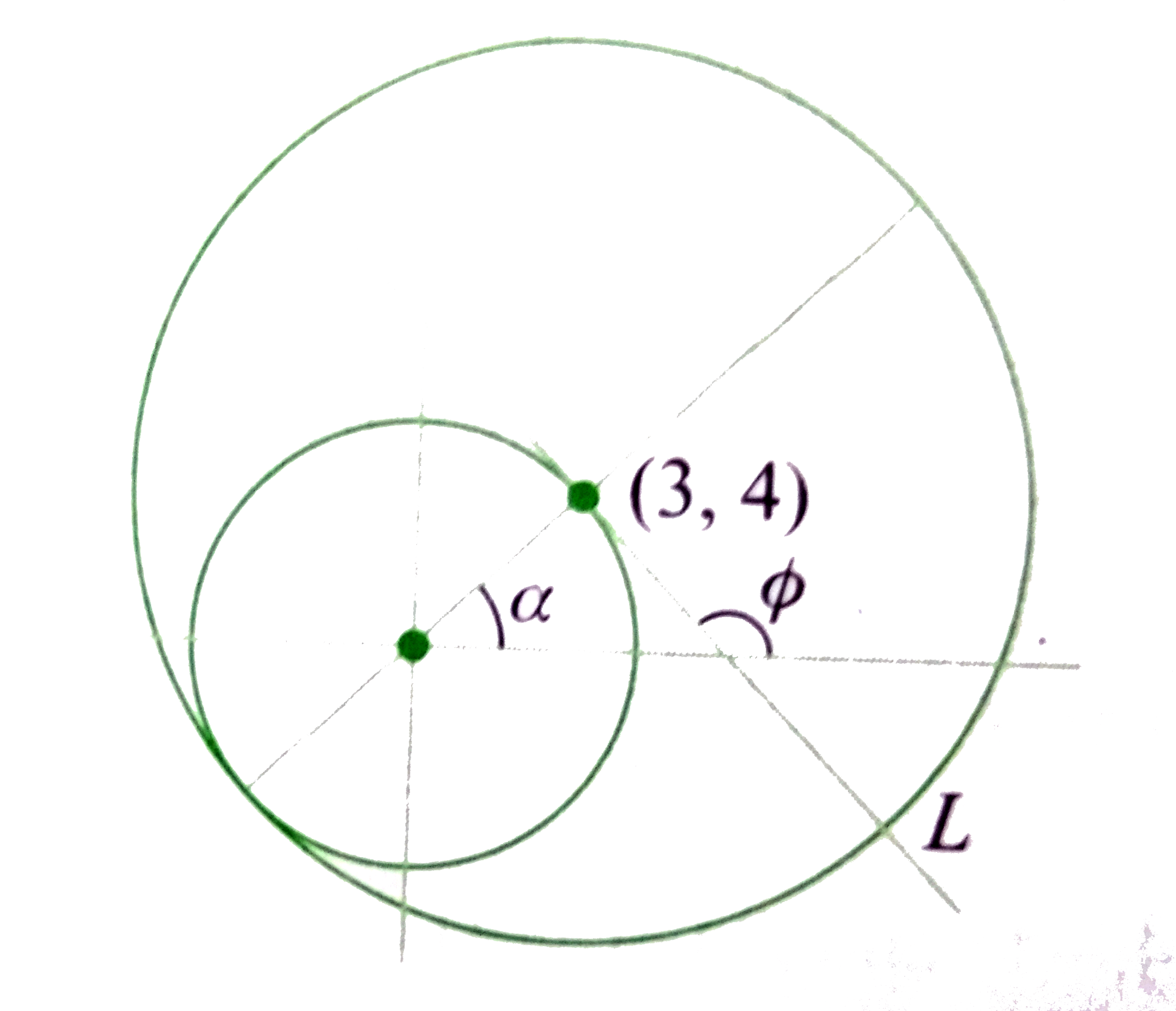 Now, if `A cap C =A` Both circle `C_(1)` and `C_(2)` must TOUCH each other internally. So, R must be 10. If `phi` is fixed and r varies and `n ( A cap B) = 1`, circle `C_(1)` touches line L. `phi =90^(@) + alpha` `:. SEC phi = sec ( 90^(@) +alpha)= - cosect alpha = - (5)/(4)` |
|