InterviewSolution
Saved Bookmarks
| 1. |
Let S be the set of all complex numbers z satisfying | -2+i|ge sqrt(5).if the complex number z_(0) is such that (1)/(|z_0-1|) is the maximum of the set {(1)/(|z-1|): ζinS}, then the principal argument of (4-z_0-overline(z)_0)/(z-overline(z)_0+2i) is |
|
Answer» `(pi)/(4)` 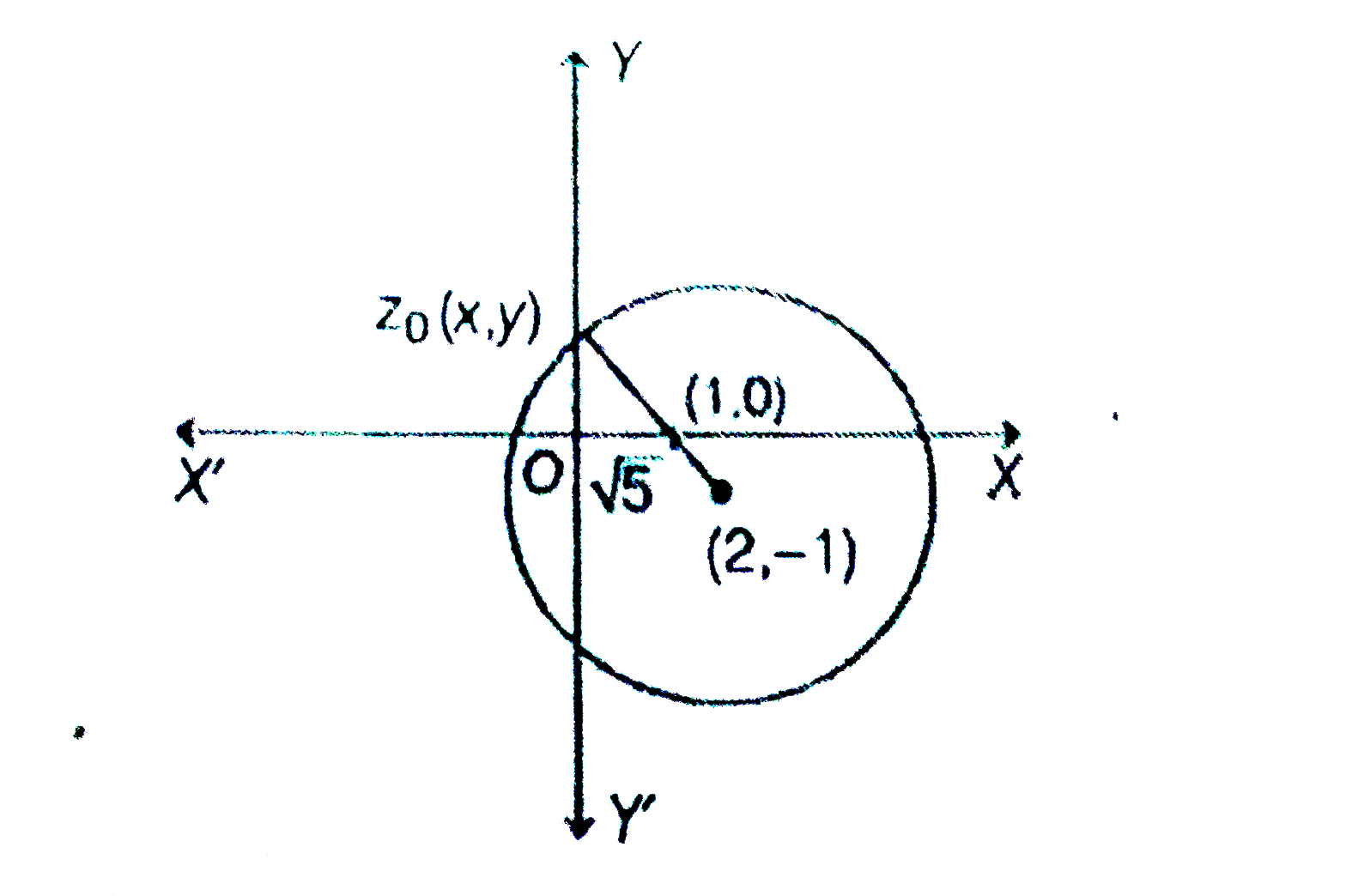 Now, for ` z_(0) in S(1)/(| z_(0)-1|)` is maximum. When `| z_0-1|` is minimum. And for this it is required that `z_0` is collinear with the points `(2,-1)` and `(1,0)` and LIES on the circumference of the circle `|ᶼ-2+i|=sqrt(5)`. So let `z_0=X+iy`, and the figure `0lt x lt 1 and y gt 0`. So, `(4-z_(0)-overline(z)_(0))/(z_0-overline(z)_(0)+2i)=(4-x-iy-x+iy)/(x+iy-x+iy+2i)=(2(2-x))/(2i(y+1))=-i((2-x)/(y+1))` `because (2-x)/(y+1)` isa positive real number, so `(4-z_0-overline(z)_0)/(z_0-overline(z)_0+2i)` is PURELY negative imaginary number. `rArr arg ((4-z_0-overset(-)z_(0))/(z_0-overset(-)z_(0)+2i))=-(pi)/(2)` . |
|