InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
Let sqrt(3)hati+hatj,hati+sqrt(3)hatj" and "betahati+(1-beta)hatj respectively be the position vectors of the points A, B and C with respect to the origin O. If distance of C from the bisector of the acute angle between OA and OB is (3)/(sqrt(2)), then the sum of all possible values of beta is(a) 1(b) 3(c) 4(c) 2 |
|
Answer» 1 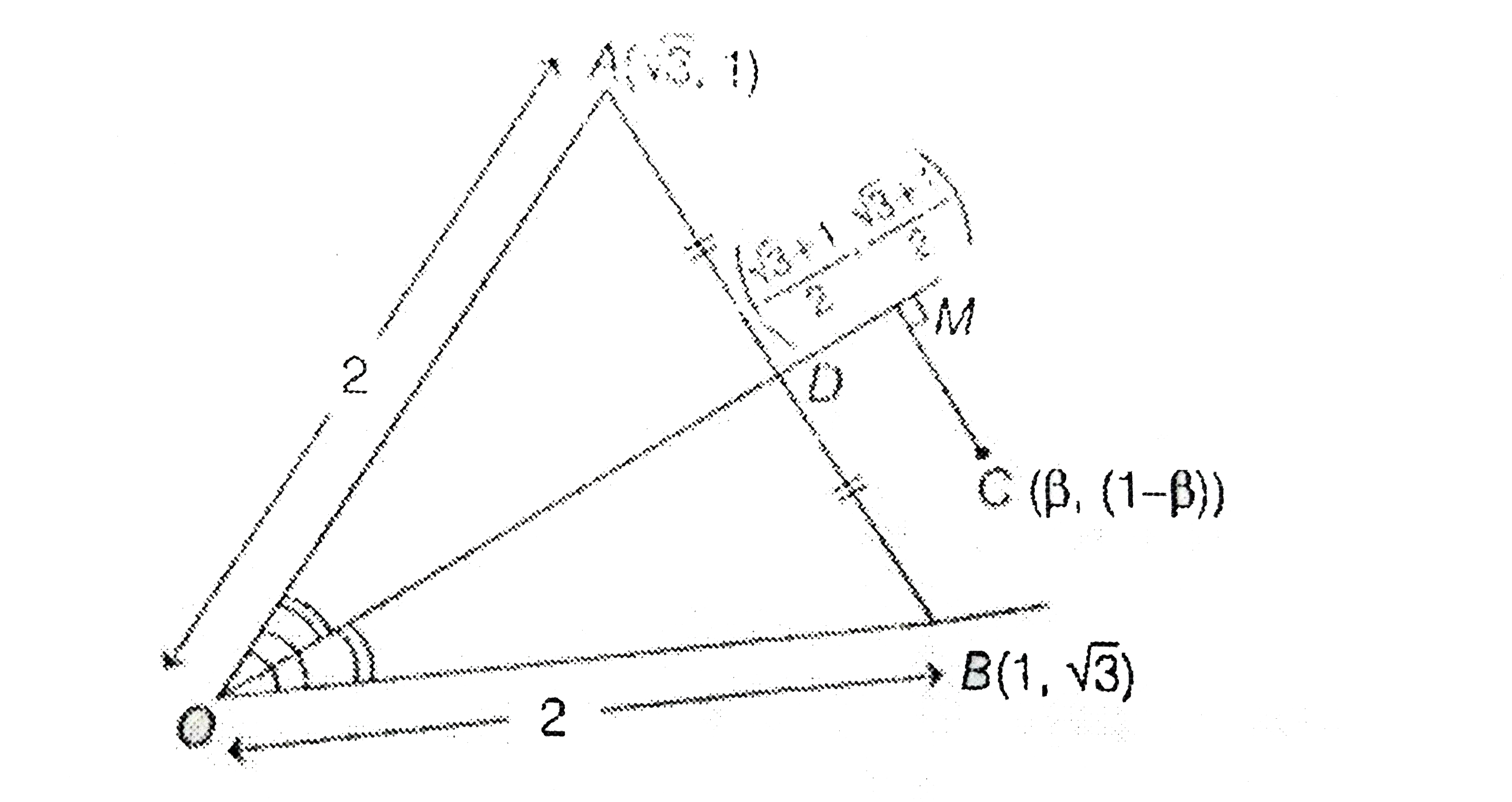 CLEARLY, angle bisector divides the sides AB in OA:OB, `i.e., 2 : 2 =1 : 1""[using angle bisector theorem]` So, D is the mid-point of AB and hence coordinates of D are `((sqrt(3)+1)/(2),(sqrt(3)+1)/(2))` Now, eauation of bisector OD is `(y-0)=(((sqrt(3)+1)/(2)-0)/((sqrt(3)+1)/(2)-0))(x-0)impliesy=x` `impliesx-y=0` According to the problem, `(3)/(sqrt(2))=CM=|(beta-(1-beta))/(sqrt(2))|` [Distance of a point `P(x_(1),y_(1))` from the line `ax+by+c=0" is "|(ax_(1)+by_(1)+c)/(sqrt(a^(2)+b^(2)))|]` `implies""|2beta-1|=3implies2beta=+-3+1` `implies""2beta=4, -2impliesbeta=2, -1` Sum of 2 and -1 is 1. |
|