InterviewSolution
Saved Bookmarks
| 1. |
Let the equation of a straight line L in complex form be abarz+baraz+b=0, where is a complex number and b is a real number then |
|
Answer» the straight line `(z-c)/a +(i(barz-barc))/a=0` makes a angle of `45^(@)` with `L` and passed through a point `c` (where `c` is a complex number) Then, `(vec(CP))/(|vecCP|)` i.e. `(z-c)/(|z-c|)` is a unit vector parallel to it Let `A(z_(1))` and `B(z_(2))` be TWO points on `baraz+abarz+b=0` then `(z_(2)-z_(1))/(|z_(2)-z_(1)|)` is a unit vector parallel to the line `abarz+baraz+b=0` `(z-c)/(|z-c|)=(z_(2)-z_(1))/(|z_(2)-z_(1)|)e^(+-i((pi)/4))` `((z-c)^(2))/((z-c)(barz-barc))=((z_(2)-z_(1))^(2))/((z_(2)-z_(1))(barz_(2)-barz_(1)))e^(+-i(pi)/2)` `((z-c)/(barz-barc))= +- i ((z_(2)-z_(1))/(barz_(2)-barz_(1)))`.......(1) `:' A(z_(1)` and `B(z_(2))` are on the line `abarz+baraz+b=0`therefore `abarz_(1)+baraz_(1)+b=0` `abarz_(2)+baraz+b=0` `implies-a/a=(z_(2))/(barz_(2))=((z_(2)-z_(1))/(barz_(2)-barz_(1)))`......(2) From EQUATION (1) and (2) we get `(z-c)/a+-(i(barz-barc))/(bara)=0` 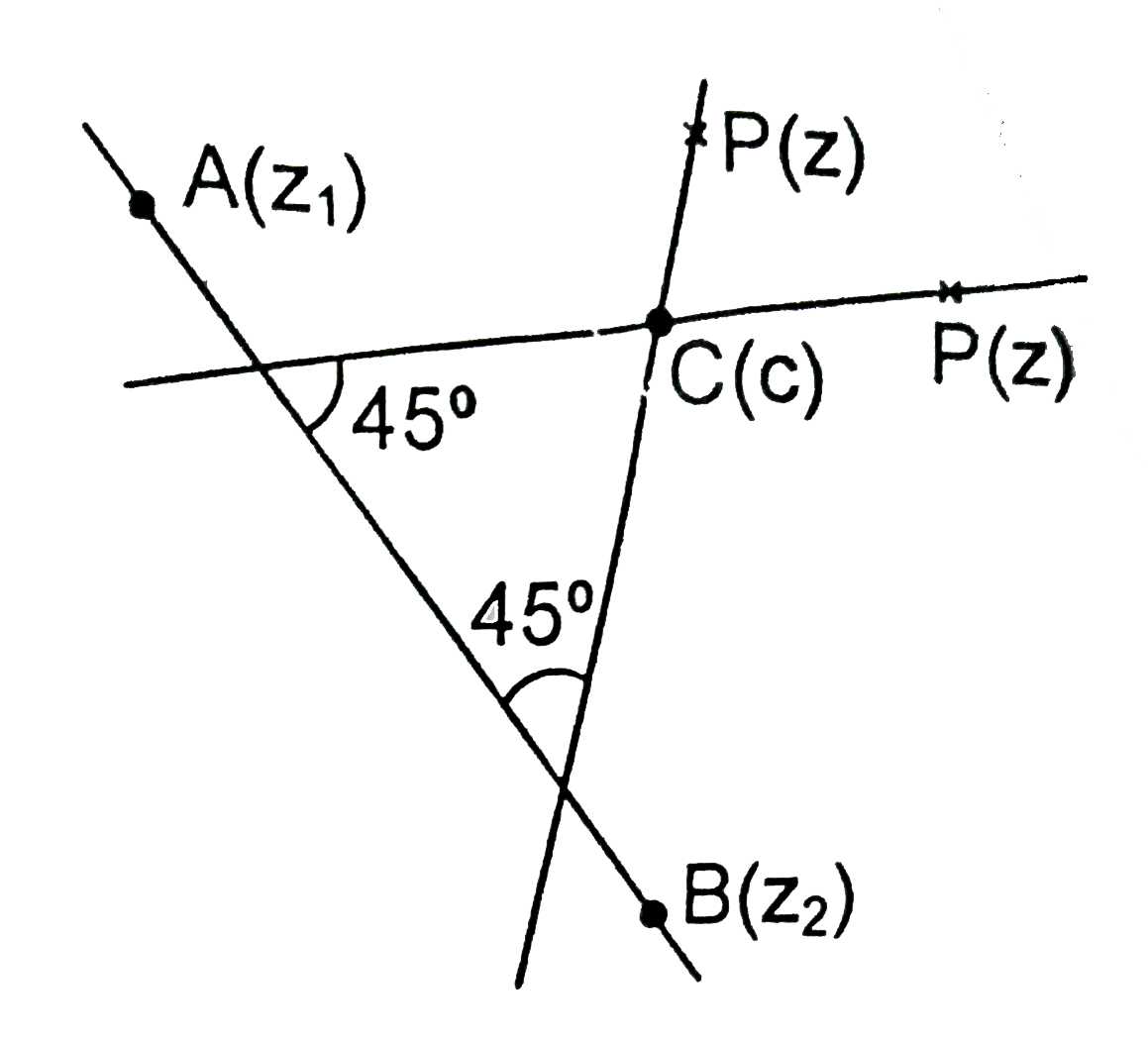
|
|