InterviewSolution
Saved Bookmarks
| 1. |
{:(,"List-I",,"List-II",),((P),"Let volume ofa tetrahedron ABCD is",(1),3,),(,(81)/(2) "cube unit and volume of parallelopiped",,,),(,"whose three coterminous edges are line",,,),(,"segment joining centroid of any face of ",,,),(,"tetrahedron with centroids of its other three",,,),(,"faces is V cubic unit. then V is",,,),((Q),"If images ofthe point (1,0,1) in the plane" ,(2),8,),(,x-y-z=1 "is (a,b,c) then 3(a-b+c)",,,),(,"is equal to",,,),((R),"Locus of all the points which are at a distance of",(3),3,),(,3 "units from the line" underset(r )(rarr)=lambda(i+j+k)" is given by",,,),(,x^(2)+y^(2)+z^(2)-xy-yz=(k)/(2) "then find"(k)/(9),,,),((S),underset(a)(rarr) "and" underset(b)(rarr)and underset(a)(rarr)underset(b)(rarr)underset(c)(rarr)"are such that" |underset(a)(rarr)|=sqrt(3)|underset(b)(rarr)|=2,(4),7,),(,"and" |underset(c)(rarr)=sqrt(6). "If"underset(a)(rarr)underset(b)(rarr)lt0underset(c)(rarr) "is perpendicular to both" ,,,),(,underset(a)(rarr) "and" underset(b)(rarr) "and" underset(a)(rarr)underset(b)(rarr)underset(c)(rarr) "form the coterminous edges of a",,,),(,"tetrahedron of unit volume then angle between" underset(a)(rarr) "and" underset(b)(rarr) ,,,),(,"is" (pi)/(q) "(where p,q are coprime number) where (p+q) is",,,):} |
|
Answer» <P>`{:(P,Q,R,S),(1,2,3,4):}` given volume of tetrahedron is |(1)/(6)[underset(a)(-)underset(b)(-)underset(c)(-)]|=(81)/(2)` |(underset(a)(-),underset(b)(-)underset(c)(-))|=3^(5)` Centroids by faces are ` G_(1)((vec(a)+vec(b) +vec(c))/(3))` ` G_(2)((vec(a)+vec(b))/(3))` G_(3)((vec(b)+vec(c))/(3))` `G_(4)((vec(c)+vec(a))/(3))` Volume of parallelopiped |vec(G_(1)G_(2))vec(G_(1)G_(3))vec(G_(1)G_(4))]|` =|[-vec(c)/(3)-vec(a)/(3)-vec(b)/(3)]|[[vec(a)vec(b)vec(c)]]/(3^(3))|=9` (Q) Let the image of the point (1,0,1) in the plane x-y-z=1 is A (a,b,c)` D.R. of AA are `(a-1,b,c-1)` D.R. of normal are `(1,-1,-1)` `(a-1)/(1)=(b)/(-1)=(c-1)/(-1)=lambda` `impliesa=lambda+1, b=-lambda, c=1-lambda` mid point of AA' lie on plane `x-y-z =1 implies lambda=(2)/(3)` `a=(5)/(3), b=(-2)/(3),c=(1)/(3) implies 3(a+b+c)=3((8)/(3))=8` (R) `vec(QP).(i+j+k)=0` implies (x-lambda)+(y-lambda)+(z-lambda)=0` lambda=(x+y+z)/(3)` 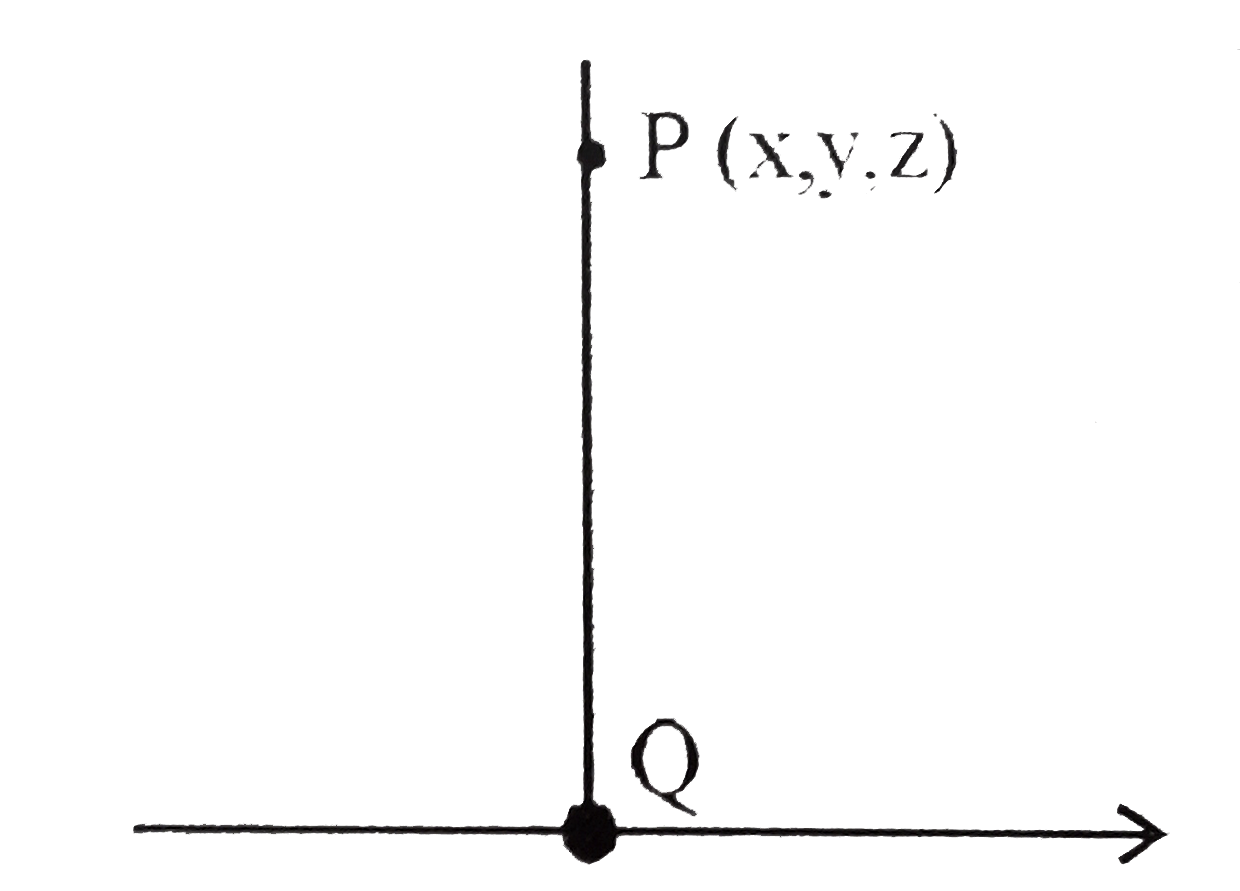 `(PQ)^(2)=9implies (x-lambda)^(2)+(y-lambda)^(2)+(z-lambda)^(2)=9` x^(2)+y^(2)+z^(2)+3lambda^(2)-2lambda(x+y+z)=9` `x^(2)+y^(2)+z^(2)+3lambda^(2)-2lambda.3lambda=9` implies x^(2)+y^(2)+z^(2)-3((x+y+z)/(3))^(2)=9` implies x^(2) +y^(2)+z^(2)-xy-yz-zx=(27)/(2)` `k=27, (k)/(9)=3` (S) underset(C)(rarr)=lambda(underset(a)(-)xxunderset(b)(-)) also` |(1)/(6)[underset(a)(-)underset(b)(-)underset(c)(-)]|=1implies |[underset(a)(-)underset(b)(-)underset(c)(-)]|=6` implies |vec((a)(-)xxvec(b)(-))vec(c)(-)|=6implies|c|^(2)/|lambda|=6` implies 6=6|lambda|implies|lambda|=1` `implies|vec((a)(-)xxvec(b)(-)).vec(c)(-)|=6implies(|c|^(2))/(|lambda|)=6` `implies 6 = 6|lambda|implies |lambda|=1` `therefore |c|^(2)=lambda^(2)|a|^(2)|b|^(2) sin^(2)THETA` `implies 6=12sin^(2)theta=theta=(3pi)/(4)(a.blt0)` `p+q=7` |
|