1.

Mass m_(1) hits & sticks with m_(2) while sliding horizontally with velocity v along the common line of centres of the three equal masses (m_(1)=m_(2)=m_(3)=m). Initially masses m_(2) and m_(3) are stationary and the spring is unstretched. Find (a) the velocities of m_(1),m_(2) and m_(3) immediately after impact. (b) the maximum kinetic energy of m_(3). (c) the minimum kinetic energy of m_(2). (d) the maximum compression of the spring.

Answer» 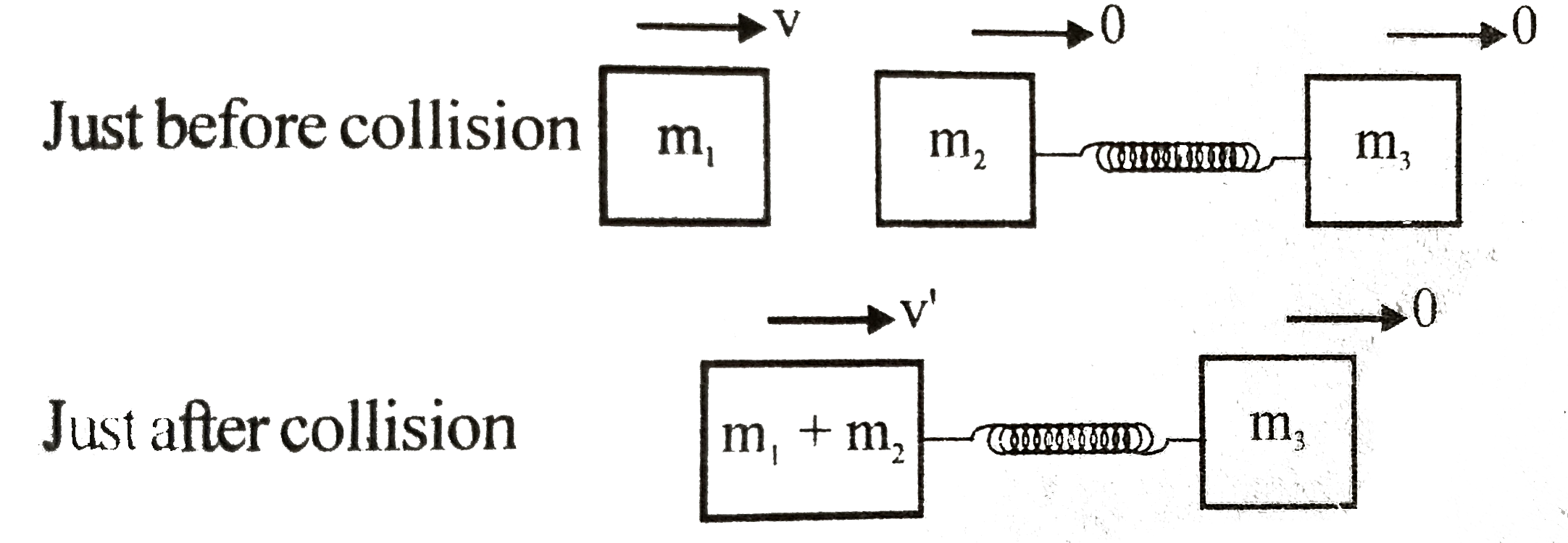<html><body><p><br/></p>Solution :Just before collision <br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_PHY_CMMC_E01_099_S01.png" width="80%"/> <br/><br/> (a) We can use conservation of momentum as spring force is not an impulsive force. <br/> `rArrmv+0=(2m)<a href="https://interviewquestions.tuteehub.com/tag/v-722631" style="font-weight:bold;" target="_blank" title="Click to know more about V">V</a>'rArr=(v)/(<a href="https://interviewquestions.tuteehub.com/tag/2-283658" style="font-weight:bold;" target="_blank" title="Click to know more about 2">2</a>)` <br/> `rArrv_(m_(1))=(v)/(2),v_(m_(2))=(v)/(2),v_(m_(3))=0` <br/> (b) Looking from <a href="https://interviewquestions.tuteehub.com/tag/cm-919986" style="font-weight:bold;" target="_blank" title="Click to know more about CM">CM</a> <a href="https://interviewquestions.tuteehub.com/tag/frome-2088630" style="font-weight:bold;" target="_blank" title="Click to know more about FROME">FROME</a> of refernce <br/> `v_(CM)=((2m)v'+m(0))/(2m+m)=(2)/(3)v'=(v)/(3)` 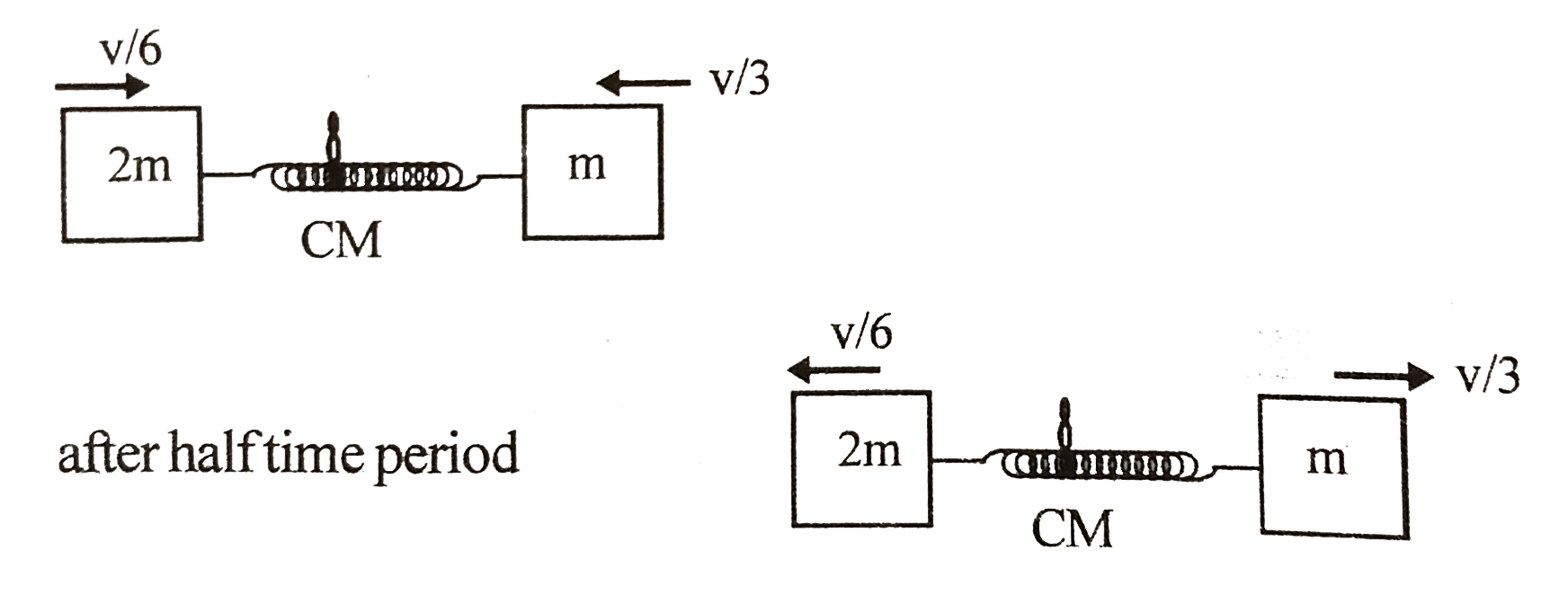<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/BSL_PHY_CMMC_E01_099_S02.png" width="80%"/> <br/> (Both the blocks will execute SHM of same time period in CM frome of reference) <br/> `rArr(v_(m_(3)))_(max)=(v)/(3)+v_(CM)=(v)/(3)+(v)/(3)=(2v)/(3)` <br/> `rArr(KE_(m_(3)))_(max)=(1)/(2)m(v_(3))_(max)^(2)=(1)/(2)m((2v)/(3))^(2)=(2mv^(2))/(9)` <br/> (c) `(v_(m_(2)))_(min)=(v)/(3)-(v)/(6)=(v)/(6)` <br/> `rArr(KE_(m_(2)))_(min)=(1)/(2)m(v_(2))_(min)^(2)=(1)/(2)m((v)/(6))^(2)=(<a href="https://interviewquestions.tuteehub.com/tag/mv-1082193" style="font-weight:bold;" target="_blank" title="Click to know more about MV">MV</a>^(2))/(72)` <br/> (d) At the time of maximum compression, both blacks will be at rest in CM frame of reference <br/> `rArr(1)/(2)kx_(max)^(2)=(1)/(2)(2m)((v)/(6))^(2)+(1)/(2)m((v)/(3))^(2)` <br/> `rArr(1)/(2)Kx_(max)^(2)=(1)/(12)mv^(2)` <br/> `rArrx_(max)=vsqrt((m)/(6k))`</body></html>


Discussion

No Comment Found

Related InterviewSolutions