1.

Show that a=(v^2)/r and hence obtain an expression for centripetal force.

Answer» <html><body><p></p>Solution :Let `vecr` and `vecr`, be the position vectors and `vecv` velocities of the <a href="https://interviewquestions.tuteehub.com/tag/object-11416" style="font-weight:bold;" target="_blank" title="Click to know more about OBJECT">OBJECT</a> when it is it point P and P. By definition, velocity at a point is <a href="https://interviewquestions.tuteehub.com/tag/along-1974109" style="font-weight:bold;" target="_blank" title="Click to know more about ALONG">ALONG</a> the tangent at that point in the direction of the motion. Since the path is <a href="https://interviewquestions.tuteehub.com/tag/circular-916697" style="font-weight:bold;" target="_blank" title="Click to know more about CIRCULAR">CIRCULAR</a>, `vecv` is perpendicular to `vecr` and `vecv` is perpendicular to `vecr` <br/> Therefore, `/_\vecv` is perpendicular to `/_\vecr`. Average acceleration `(/_\vecv)/(/_\t)` is perpendicular to `/_\vecr` <br/> The magnitude of `veca` is, by definition, given by `|veca|=lim_(/_\t to0)(/_\vecv)/(/_\t)` <br/> The <a href="https://interviewquestions.tuteehub.com/tag/triangle-1427233" style="font-weight:bold;" target="_blank" title="Click to know more about TRIANGLE">TRIANGLE</a> formed by the position vectors is similarly to the triangle formed by the velocity vectors. 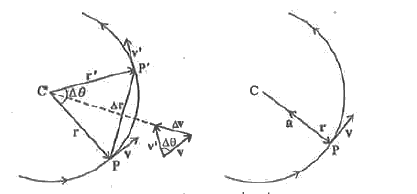<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/SPH_ABT_PHY_QB_XI_C04_E04_006_S01.png" width="80%"/> <br/> i.e, `(|/_\vecv|)/v=(|/_\vecr|)/r "or"|/_\vecv|=v(|/_\vecr|)r` <br/> Therefore, `|veca|=lim_(|/_\vecv)/(/_\t)=lim_(/_\t to0)(v|/_\vecr|)/(r/_\t)=(vecv)/(r)lim_(/_\t to0)(|/_\vecr|)/(/_\t)` <br/> If `/_\t` is very small, `/_\theta` will also small. The arc PP' is approximately equal to `|/_\vecr|` <br/> i.e., `lim_(/_\t to0)(|/_\vecr|)/(/_\t)=v` Thus, centripetal acceleration `|veca|=v/fv=(v^2)/(r)` and `veca=v/r(dvecr)/(dt)` <br/> The centripetal acceleration is always <a href="https://interviewquestions.tuteehub.com/tag/directed-440230" style="font-weight:bold;" target="_blank" title="Click to know more about DIRECTED">DIRECTED</a> towards the centre. The centripetal force=ma.</body></html>


Discussion

No Comment Found

Related InterviewSolutions