1.

Show that the coefficient of area expansions, (DeltaA//A)//DeltaT, of a rectangular sheet of the solid is twice its linear expansively, alpha_(l).(alpha_(l)=10^(-5)K^(-1))

Answer» <html><body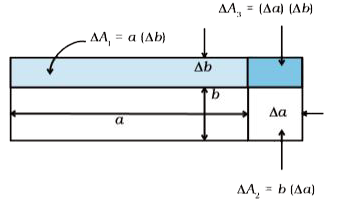><p></p>Solution :<img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_GUJ_PHY_XI_P2_C11_SLV_001_S01.png" width="80%"/> <br/> Consider a <a href="https://interviewquestions.tuteehub.com/tag/rectangular-1180623" style="font-weight:bold;" target="_blank" title="Click to know more about RECTANGULAR">RECTANGULAR</a> sheet of the solid material of length a and <a href="https://interviewquestions.tuteehub.com/tag/breadth-903817" style="font-weight:bold;" target="_blank" title="Click to know more about BREADTH">BREADTH</a> b (Fig. 11.8). When the <a href="https://interviewquestions.tuteehub.com/tag/temperature-11887" style="font-weight:bold;" target="_blank" title="Click to know more about TEMPERATURE">TEMPERATURE</a> <a href="https://interviewquestions.tuteehub.com/tag/increases-1040626" style="font-weight:bold;" target="_blank" title="Click to know more about INCREASES">INCREASES</a> by`Delta T, a `Increases by `Delta a = alpha_(1) a Delta T` andbincreases by `Delta b = alpha_(1), b Detla T`. From Fig. 11.8, the increase in area<br/> `Delta A = DeltaA_(1) + DeltaA_(2) + DeltaA_(3)` <br/> `DeltaA = a Deltab + b Delta a + (Delta a) (Deltab)` <br/> ` = a alpha_(1) b DeltaT + b alpha_(1) a DeltaT + (alpha_(1))^(2) <a href="https://interviewquestions.tuteehub.com/tag/ab-360636" style="font-weight:bold;" target="_blank" title="Click to know more about AB">AB</a> (Delta T)^(2)` <br/> ` = alpha_(1) ab DeltaT (2 +alpha_(1) DeltaT) = alpha_(1) A DeltaT (2 + alpha_(1) DeltaT)` <br/> Since `alpha_(1) approx 10^(-5) K^(-1)`,from Table 11.1 , the product `alpha_(1) Delta T ` for fractional temperature is small in comparision with 2 and may be neglected. <br/> Hence, <br/> `((Delta A)/A) 1/(Delta T) approx 2alpha_(l) `</body></html>


Discussion

No Comment Found

Related InterviewSolutions