1.

The acceleration of a bus is given by a_x(t)=at, where a=1.2ms^-2. a. If the bus's velocity at time t=1.0s is 5.0ms^-1, what is its velocity at time t=2.0s? b. If the bus's position at time t=1.0s is 6.0m, what is its position at time t=2.0s? c. Sketch a_x-t, v_x-t, and x-t graphs for the motion.

Answer» <html><body><p></p><a href="https://interviewquestions.tuteehub.com/tag/solution-25781" style="font-weight:bold;" target="_blank" title="Click to know more about SOLUTION">SOLUTION</a> :a. The <a href="https://interviewquestions.tuteehub.com/tag/velocity-1444512" style="font-weight:bold;" target="_blank" title="Click to know more about VELOCITY">VELOCITY</a> `v_2` at time `t` <br/> `v_2=v_1+int_(t_1)^(t)atdt` <br/> `=v_1+alpha/2(t^2-t_1^2)` <br/> `=v_1-alpha/2t_1^2+alpha/2t^2` <br/> `=(5.0ms^-1)-(0.6ms^-3)(1.0s)^2+(0.6ms^-3)t^2` <br/> `=(4.40ms^-1)+(0.6ms^-3)t^2`. <br/> At `t_2=2.0s`, the velocity is `v_2=(4.40ms^-1)+(0.6ms^-3)(2.0s)^2` <br/> `=6.80ms^-1`, or `6.8ms^-1` to two significant figures. <br/> b. the <a href="https://interviewquestions.tuteehub.com/tag/position-1159826" style="font-weight:bold;" target="_blank" title="Click to know more about POSITION">POSITION</a> `x_2` as a function of time is <br/> `x_2=x_1+int_(t_1)^tv_xdt` <br/> `=(6.0m)+int_(t_1)^t(4.40ms^-1)+(0.6ms^-3)t^(2))dt` <br/> `=(6.0m)+(4.40ms^-1)(t-t_1)+((0.6ms^-3))/(3)(t^3-t_1^3)` <br/> At `t=2.0s`, and with `t_1=1.0s`, <br/> `<a href="https://interviewquestions.tuteehub.com/tag/x-746616" style="font-weight:bold;" target="_blank" title="Click to know more about X">X</a>=(6.0m)+(4.40ms^-1)[(2.0s)-(1.0s)]` <br/> `+(0.20ms^-3)[(2.0s)^3-(1.0s)^3]=11.8m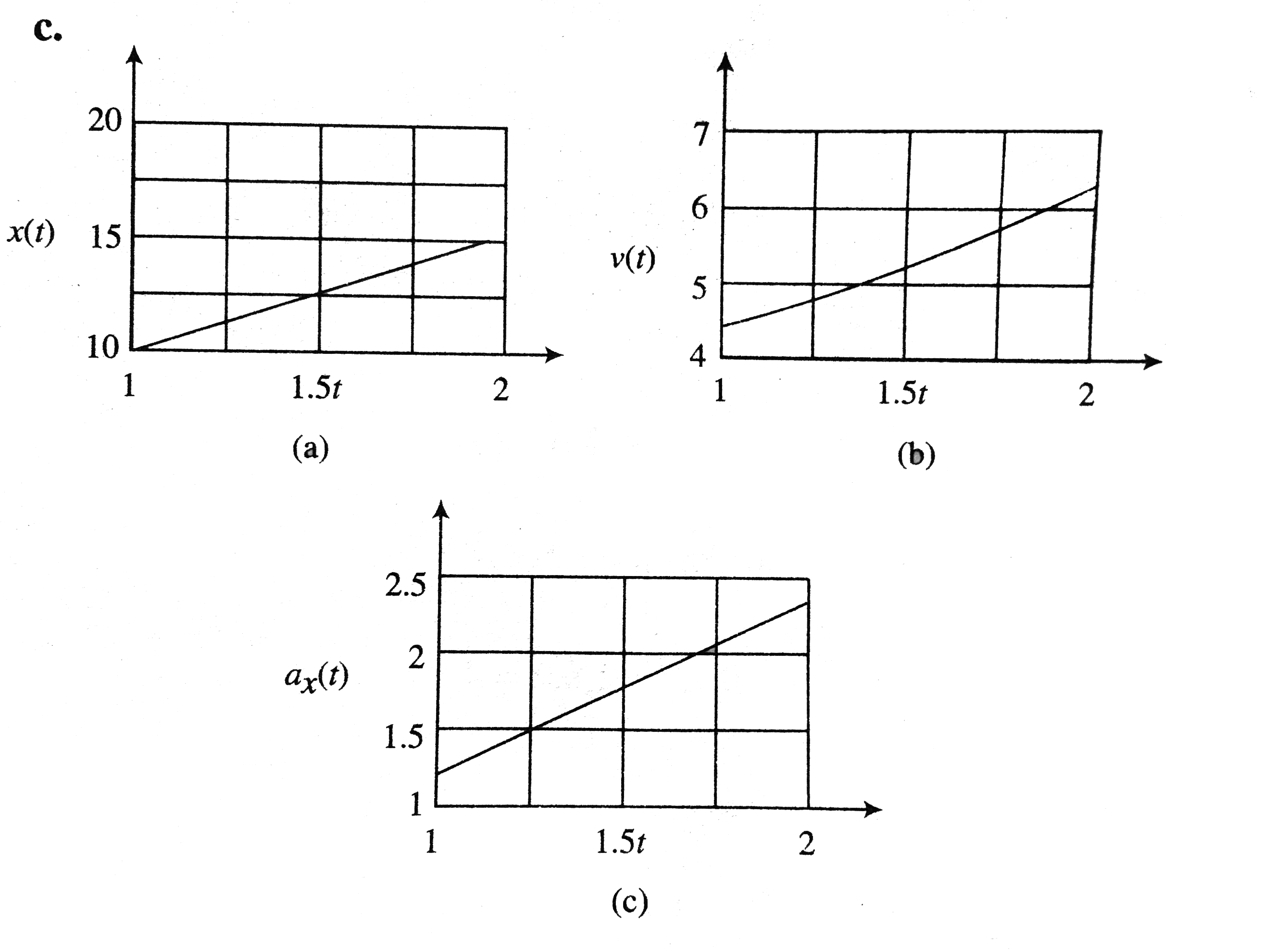` <br/> <a href="https://interviewquestions.tuteehub.com/tag/c-7168" style="font-weight:bold;" target="_blank" title="Click to know more about C">C</a>. <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V01_C02_E01_033_S01.png" width="80%"/></body></html>


Discussion

No Comment Found

Related InterviewSolutions