InterviewSolution
Saved Bookmarks
| 1. |
The straight line x + 2y = 1 meets the coordinate axes at A and B. A circle is drawn through A,B and the origin. Then, the sum ofperpendicular distances from A and B on the tangent to the circle at the origin is |
|
Answer» `2sqrt5` 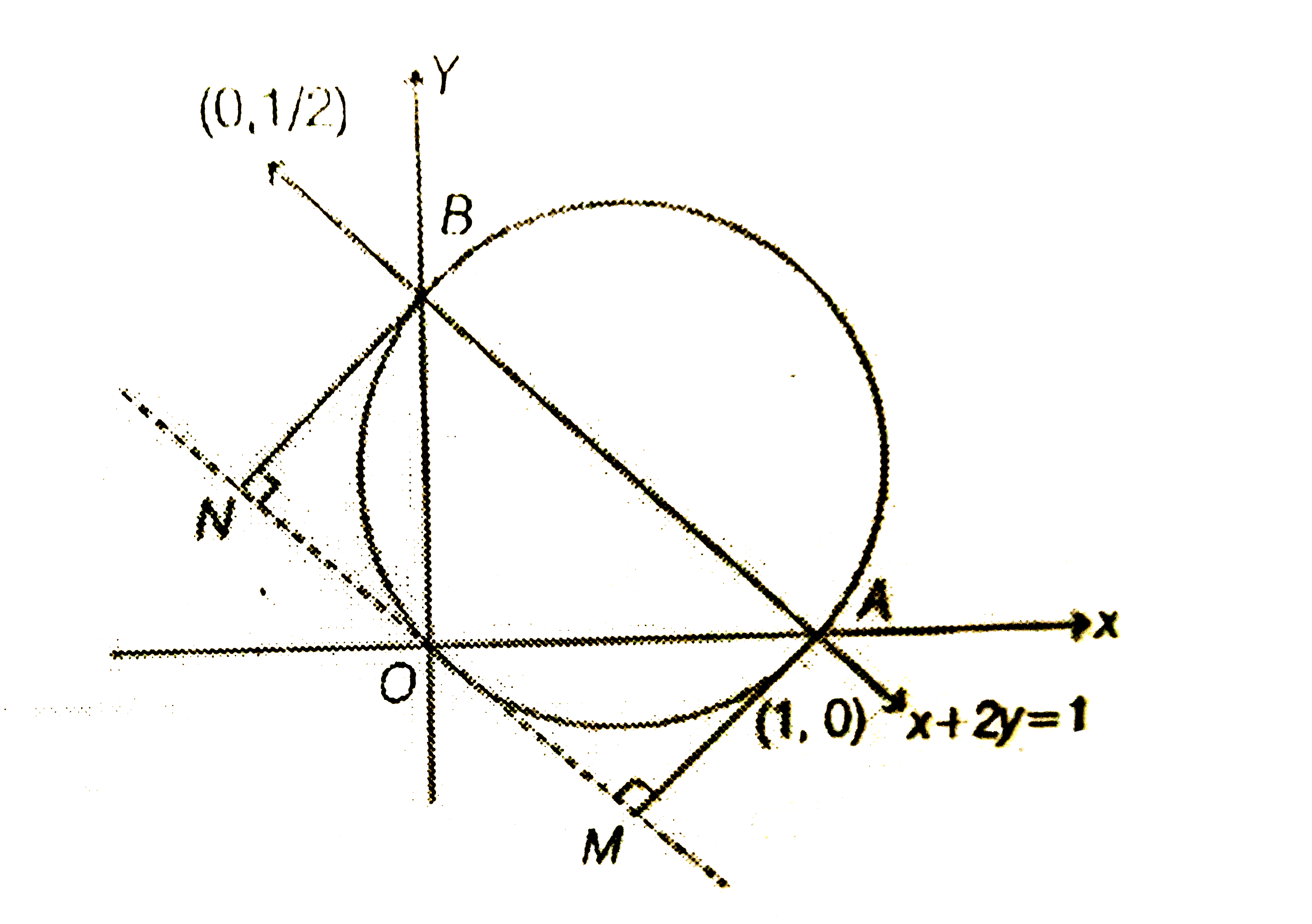 From figure, equation of circle (DIAMETER form) is `(X-1)(x-0)+(y-0)((y-(1)/(2))=0` `rArr x^(2) + y^(2) -x -(y)/(2)=0` Equation of tangent at (0, 0) is `x+(y)+(2) = 0` `[therefore" equation of tangent at "(x_(1),y_(1)) " is given by " T=0 " Here ", T = 0` `rArr "xx"_(1)+yy_(1)-(1)/(2)(x+x_(1))-(1)/(4)(y+y_(1))=0]` `rArr2x + y =0 ` Now, `AM=(|2.1+1.0|)/(sqrt5)=(2)/(sqrt5)` `[therefore " distance of a point " P(x_(1), y_(1))`from a line `ax+by + c=0 " is " (|ax_(1)+by_(1)+c|)/(sqrt(a^(2)+b^(2)))]` and `BN = (|2.0+1((1)/(2))|)/(sqrt5)=(1)/(2sqrt5)` `therefore AM+BN=(2)/(sqrt5)+(1)/(2sqrt5)=(4+1)/(2sqrt5)=(sqrt5)/(2)` |
|