InterviewSolution
Saved Bookmarks
| 1. |
The tagents at any point P of the circle x^(2)+y^(2)=16 meets the tangents at a fixed point A at T. Point is joined to B,the other end of the diameter, through, A. Which of the following does not change by changing the radius of the circle ? |
|
Answer» Coordinartes of foci The equation of AP is `y=(sin theta)/(cos theta-1)(x-4)""(2)` 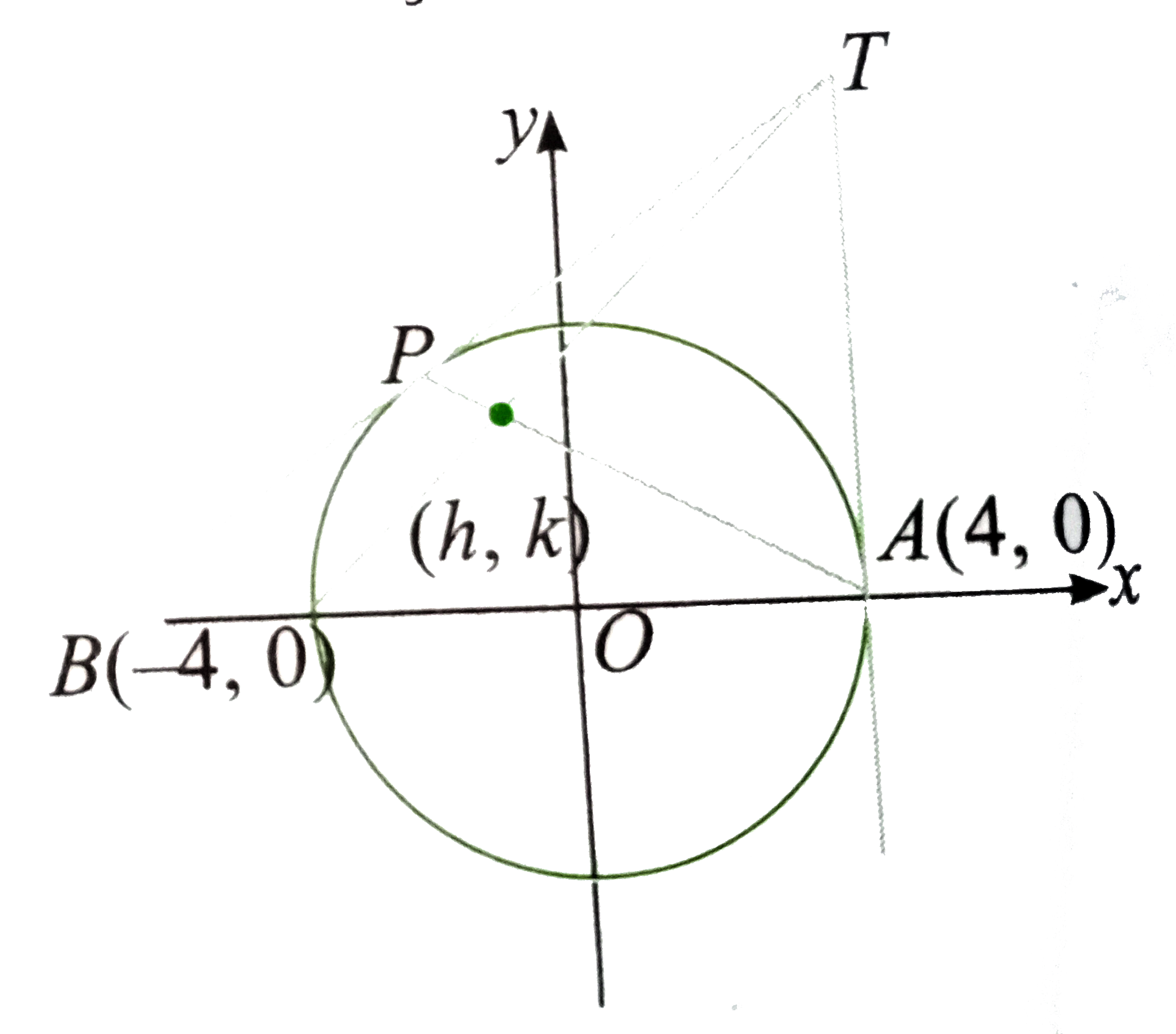 From (1), the coordinates of the point T are given by `(4,(4(1-costheta))/(sin theta))` The equation of BT is `y=(1-cos theta)/(2 sin theta)(x+4)""(3)` LET (h,k) be the point of intersection of the lines (2), and (3). Then we have `k^(2)=-(1)/(2)(h^(2)-16)` or `(h^(2))/(16)+(y^(2))/(8)=1` Therefore, the locus of (h,k) is `(x^(2))/(16)+(y^(2))/(8)=1` Which is an ELLIPSE with eccehntrically `e=1//sqrt(2)` Sumof focal distance of any points is 2a=8 Considering the circle `x^(2)+y^(2)=a^(2)`, we find the that the eccentricity of the ellipse is `1sqrt(2)` which is contant and does not change by changing the radius of the circle |
|