1.

Two balls of masses m_(1)=100 g and m_(2)=300 g are suspended from point A by two equal inextensible threads, each of length l=32/35m. Ball of mass m_(1) is drawn aside and held at the same level as A but at a distance (sqrt(3)/2)l from A, as shown in Fig. When ball m_(1) is released, it collides elastically with the stationary ball of mass m_(2). Velocity u_(1) with which the hall of mass m_(1) collides with the other ball is

Answer» <html><body><p>`1m//s`<br/>`2m//s`<br/>`3m//s`<br/>`4m//s`</p>Solution :Ball of <a href="https://interviewquestions.tuteehub.com/tag/mass-1088425" style="font-weight:bold;" target="_blank" title="Click to know more about MASS">MASS</a> `m_(<a href="https://interviewquestions.tuteehub.com/tag/1-256655" style="font-weight:bold;" target="_blank" title="Click to know more about 1">1</a>)` falls freely till thread <a href="https://interviewquestions.tuteehub.com/tag/becomes-1994370" style="font-weight:bold;" target="_blank" title="Click to know more about BECOMES">BECOMES</a> taut. At that instant inclination `theta` of the thread with the vertical be given by<br/> `sintheta=(((sqrt(3))/2l))/l=(sqrt(3))/2` or `theta=60^(@)` <br/> Ball of mass `m_(1)` falls freely through height. 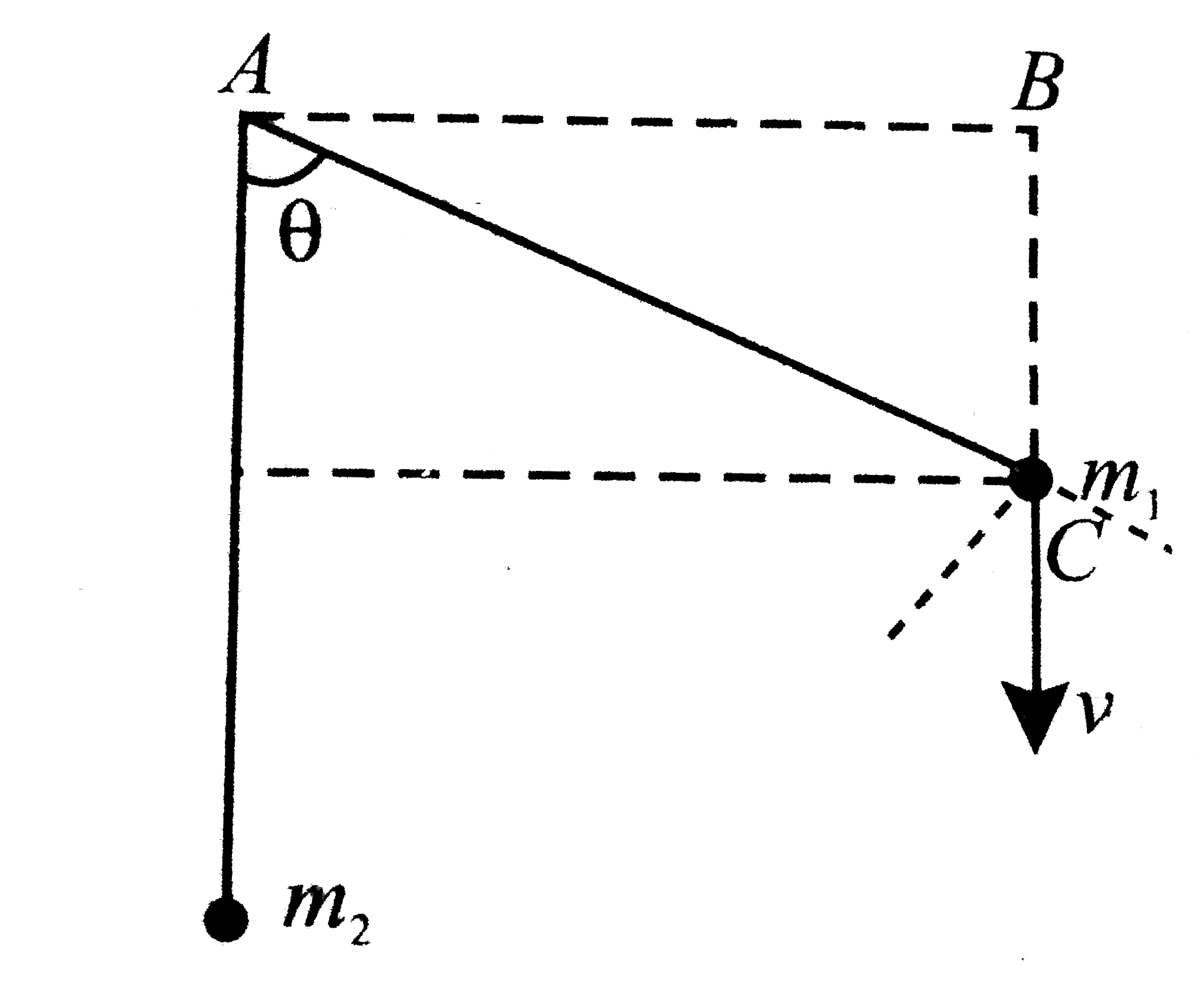<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_VOL2_C01_E01_334_S01.png" width="80%"/> <br/> Velocity of this ball at this instant is `<a href="https://interviewquestions.tuteehub.com/tag/v-722631" style="font-weight:bold;" target="_blank" title="Click to know more about V">V</a>=sqrt(2gxxl/2)=sqrt(gl)` <br/> It can be resolved into two components. <br/> i. `v cos theta`, along the thread. But thread is inextensible, hence this component decreases to zero (due to tension developed in the thread). <br/> ii. `v sin theta`, perpendicular to the thread. Due to this component ball starts to move along a circle whose centre is at `A`. <br/> According to law of conservation of energy, <br/> Kinetic energy of ball `m_(1)` just before collision `=` Its kinetic energy at `AC +` Further loss of its potential energy <br/> `1/2m_(1)u_(1)^(2)=1/2m_(1) (sqrt(gl)sintheta)^(2)+m_(1)<a href="https://interviewquestions.tuteehub.com/tag/g-1003017" style="font-weight:bold;" target="_blank" title="Click to know more about G">G</a>(l-lcostheta)` <br/> `u_(1)=4m//s` <br/> According to law of conservation of momentums <br/> `m_(1)v_(1)+m_(2)v_(2)=m_(1)u_(1)+m_(2)u_(2)` <br/> and coefficient of restitution `e=(v_(2)-v_(1))/(u_(2)-u_(1))=1` <br/> substituting `u_(1)=4 m//s, u_(2)=, m_(1)=0.1 kg` and `m_(2)=0.3kg, v_(2)=2m//s,` the height to which it rises is <br/> `h=v_(2)^(2)/(2g)=0.20m`</body></html>


Discussion

No Comment Found

Related InterviewSolutions